Match the column:

The correct Answer is:A-P, S; B-P, R; C-Q, R
Topper's Solved these Questions
Similar Questions
A vector has a magnitude x . If it is rotated by an angle θ then magnitude of change in vector is nx. Match the following two columns.
Column I Column II(A)θ=60∘(P)n=√3(B)θ=90∘(Q)n=1(C)θ=120∘(r)n=√2(D)θ=180∘(s)n=2View SolutionA vector has a magnitude x . If it is rotated by an angle θ then magnitude of change in vector is nx. Match the following two columns.
Column I Column II(A)θ=60∘(P)n=√3(B)θ=90∘(Q)n=1(C)θ=120∘(r)n=√2(D)θ=180∘(s)n=2View Solution
Knowledge Check
- Question 1 - Select One
If θ is the angle between two vectors A and B , then match the following two columns.
Column I Column II(A)A.B=|A×B|(P)θ=90∘(B)A.B=B2(Q)θ=0∘or180∘(C)|A+B|=|A−C|(r)A=B(D)|A×B|=AB(s)NoneAA→s, B→q,r , C→p, D→pBA→p, B→q,r , C→p, D→sCA→s, B→q,r , C→s, D→pDA→s, B→q , C→r, D→p
A disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
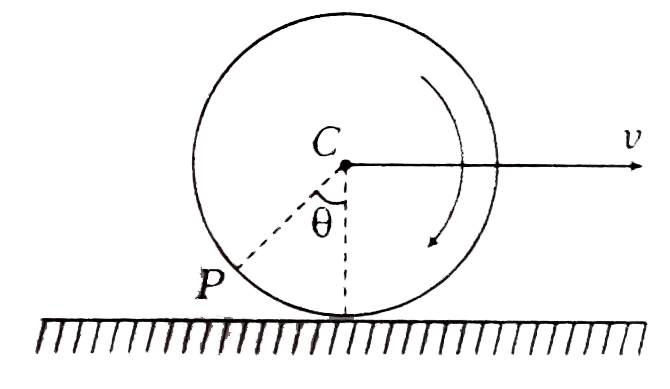
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3vView SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns

Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3vView SolutionIf θ is the abgle between two vectors A and B , then match the following two columns.
Column I Column II(A)A.B=|A×B|(P)θ=90∘(B)A.B=B2(Q)θ=0∘or180∘(C)|A+B|=|A−C|(r)A=B(D)|A×B|=AB(s)NoneView SolutionColumn IColumn II(a)Work(p)WF(b)Kinetic energy(q)mgh(c)Potential energy(r)12mv2(d)Displacement(s)F×S
View SolutionA particle is executing simple harmonic motion with frequency f. Match the columns.
Column-IColumn-II(A)Zero(p)Frequency with which kinetic energy of particle osciallates(B)t(q)Frequency with which potential energy of particle oscillates(C)2f(r)Frequency with which difference between kinetic and potential energy of oscillates(D)4f(s)Frequency with which velocity of paritcle osciallates (t)Frequency with which total mechanical energy oscillatesView SolutionA particle is executing simple harmonic motion with frequency f. Match the columns.
Column-IColumn-II(A)Zero(p)Frequency with which kinetic energy of particle osciallates(B)t(q)Frequency with which potential energy of particle oscillates(C)2f(r)Frequency with which difference between kinetic and potential energy of oscillates(D)4f(s)Frequency with which velocity of paritcle osciallates (t)Frequency with which total mechanical energy oscillatesView SolutionSuppose a function f(x) satisfies the following conditions
f(x+y)=f(x)+f(y)1+f(x)f(y),∀x,yandf'(0)=1. Also,−1<f(x)<1,∀x∈R.
Match the entries of the following two columns.
Column IColumn II(A)f(x) is differentiable over the set(p)R−(−1,0,1)(B)f(x) increases in the interval(q)R(C)Number of the solutions of f(x) = 0 is(r)0(D)The value of the limitlimx→∞[f(x)]xis(s)1View Solution

