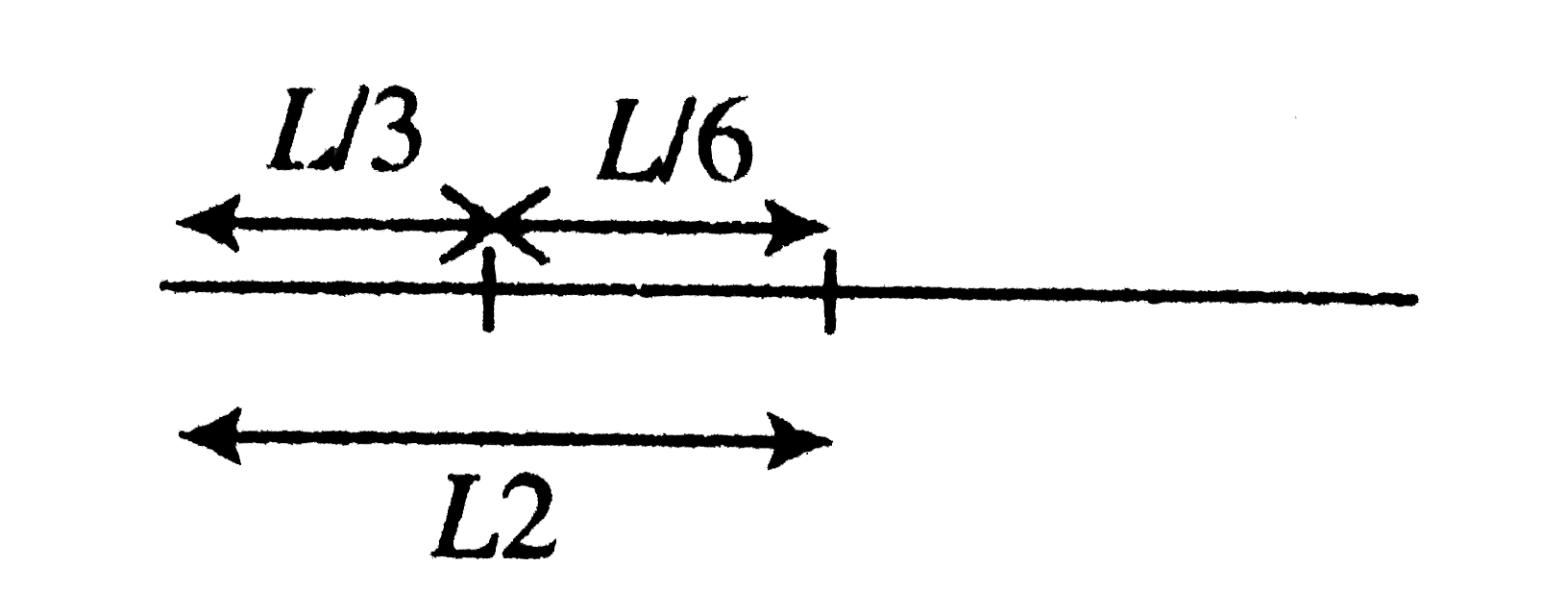
Moment of inertia of a uniform rod of length $L$ and mass $M$ , about an axis passing through $L / 4$ from one end and perpendicular to its length is

A

$\frac{M L^{2}}{3}$

B

$\frac{M L^{2}}{6}$

C

$\frac{M L^{2}}{9}$

D

$\frac{M L^{2}}{12}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Using theorem of parallel axes
$I = \frac{M L^{2}}{12} + M {(\frac{L}{6})}^{2}$
$I = \frac{M L^{2}}{12} + \frac{M L^{2}}{36} = \frac{M L^{2}}{9}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The radius of gyration of an uniform rod of length $l$ about an axis passing through one of its ends and perpendicular to its length is.
A $\frac{l}{\sqrt{2}}$
B $\frac{l}{3}$
C $\frac{l}{\sqrt{3}}$
D $\frac{l}{2}$

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 1-Single Correct

Home
Ask Doubt
Profile