Obtain an expression for the electric field intenstiy at a point on the equatorial line of an electric dipole.Solution in Kannada

Video Solution

Text Solution

Verified by Experts

Consider an electric dipole consisting of two point charges +q and -q separated by a small distance 2a.
We have to find the electric field intensity at p on the equatorial line of the dipole when $θ p = r$ .
$E_{1}$ is electric field intensity at P due to charge +q is ,
$| E_{1} | = \frac{1}{4 π ε_{0}} \frac{q}{A P^{2}}$ where $A P^{2} = a^{2} + r^{2}$
$| E_{1} | = \frac{1}{4 π ε_{0}} \frac{q}{a^{2} + r^{2}}$
The magnitude of the electric field intensity at P due to charge -q is
$| E_{2} | = \frac{1}{4 π ε_{0}} \frac{q}{a^{2} + r^{2}}$
The direction of ${\to E}_{1}$ is away from the charge +q and the direction of ${\to E}_{2}$ is towards the each other charge -q as shown ${\to E}_{1}$ and ${\to E}_{2}$ can be resolved into two components . The components normal to the dipole axis cancel away . The components along the dipole axis add up.
$∴ {\to E}_{1} = (E_{1} cos θ + E_{2} cos θ) - ˆ P$
Here the direction of $\to E$ is opposite to the dipole monent P
$∴ - ˆ P$ is a unit vector .
$\to E = (E_{1} + E_{2}) cos θ - ˆ P ∵ | E_{1} | = | E_{2} |$
$\to E = (\frac{1}{4 π ε_{0}} \frac{q}{(a^{2} + r^{2})} + \frac{1}{4 π ε_{0}} \frac{q}{(a^{2} + r^{2})}) cos θ - ˆ P$
From the figure , cos $θ = \frac{1}{{(a^{2} + r^{2})}^{1 / 2}} - ˆ P$
$\to E = \frac{1}{4 π ε_{0}} \frac{q}{a^{2} + r^{2}} [1 + 1] \frac{a}{{(a^{2} + r^{2})}^{1 / 2}} - ˆ P$
$= 2 \frac{1}{4 π ε_{0}} \frac{q a}{{(a^{2} + r^{2})}^{3 / 2}} - ˆ P ∵ P = q \times 2 a$
$= \frac{1}{4 π ε_{0}} \frac{P}{{(a^{2} + r^{2})}^{3 / 2}} - ˆ P$
$\to E = \frac{1}{4 π ε_{0}} \frac{\to P}{{(a^{2} + r^{2})}^{3 / 2}} ∵ ˆ P = \frac{\to P}{P}$
a < < < r So, a can be neglected .
$\to E = \frac{1}{4 π ε_{0}} . \frac{\to P}{{(r^{2})}^{3 / 2}} - \frac{\to P}{P}$
$\to E = - \frac{1}{4 π ε_{0}} \frac{\to P}{r^{3}}$

Updated on:21/07/2023

|

Class 12 PHYSICS PUE BOARD MODEL QUESTION PAPER 1

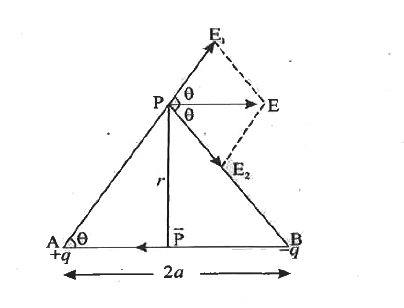
Topper's Solved these Questions

Similar Questions

SUBHASH PUBLICATION-PUE BOARD MODEL QUESTION PAPER 1-QUESTION

Home
Ask Doubt
Profile