Obtain the expression for electric field due to an uniformly charge spherical shell. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Electric field due to a uniformly charged spherical shell: Consider a uniformly charged spherical shell of radius R and total charge Q. The electric field at points outside and inside the sphere is found using Gauss law.
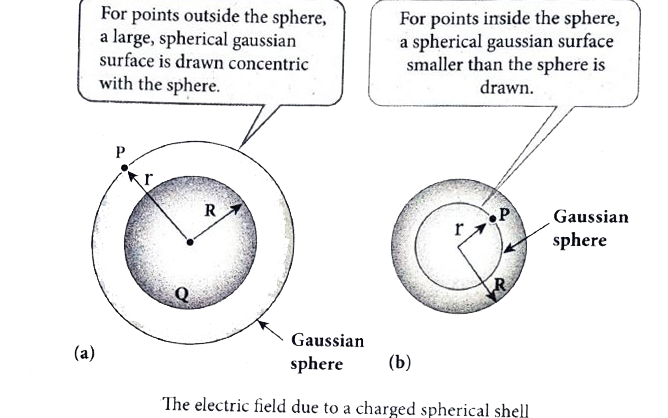
Case (a) At a point outside the shell (r > R): Let us choose a point P outside the shell at a distance r from the center as shown in figure (a). The charge is uniformly distributed on the surface of the sphere (spherical symmetry). Hence the electric field must point radially sphere equation (2). In vector form ...(3) outward if Q > 0 and point radially inward if Q < 0. So we choose a spherical Gaussian surface of radius r and the total charge enclosed by this Gaussian surface is Q. Applying Gauss law,
$\oint \to E . d \to A = \frac{Q}{e_{0}}$ ...(1)

The electric field $\to E$ and $d \to A$ point in the same direction (outward normal) at all the points on the Gaussian surface. The magnitude of E is also the same at all points due to the spherical symmetry of the charge distribution.
Hence $E \oint d A Gaussian Surface = \frac{Q}{e_{0}}$
But $\oint d A Gaussian Surface$ = total area of Gaussisn surface = $4 π r^{2}$ . Substuting this value in equation (2)
$E .4 π r^{20 = \frac{Q}{e_{0}}}$
or $E = \frac{1}{4 π e_{0}} \frac{Q}{r^{2}}$
In vector form $\to E = \frac{1}{4 π e_{0}} \frac{Q}{r^{2}} ˆ r$
The electric held is radially outward if Q > () nnd radially inward if Q < 0, From equation (3), we infci that the electric field at a point outside the shell will be same as if the entire charge Q is concentrated at (he center ol the spherical shell. (A similar result is observed in gravitation, for giavitational foice due to a spherical shell with mass M)
Case (b): At a point on the surface of the spherical shell (r = R): The electrical field at points on the spherical shell (r= R) js given by
$\to E = \frac{Q}{4 π e_{0} R^{2}} ˆ r$
Case (c) At a point inside the spherical shell (r < R): Consider a point P inside the shell at a distance r from the center. A Gaussian sphere of radius r is constructed as shown in the figure (b). Applying Gauss law
$\oint Gaussian Surface \to E . d \to A = \frac{Q}{e_{0}}$
$E = 4 π r^{2} = \frac{Q}{e_{0}}$ ...(5)
Sincew Gaussian surface encloses no charge, So Q=0. The equation (5) becomes
E=0, (rThe electric field due to the uniformly charged spherical shell is zero at all points inside the shell.

Updated on:21/07/2023

|

Class 12 PHYSICS SAMPLE PAPER -10 (SOLVED)

Topper's Solved these Questions

Similar Questions

FULL MARKS-SAMPLE PAPER -10 (SOLVED)-PART - IV

Home
Ask Doubt
Profile