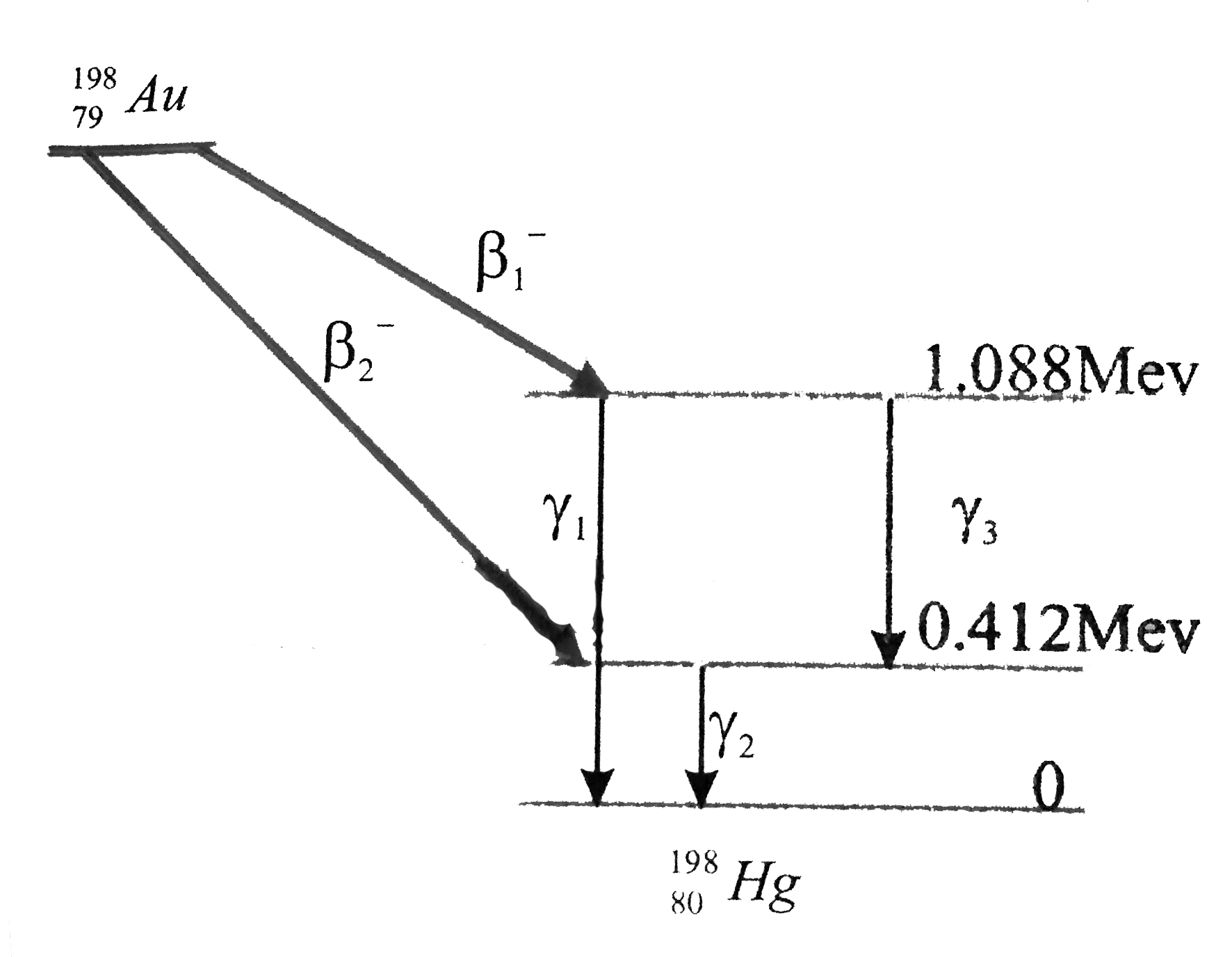
Obtain the maximum kinetic energy of $β$ - particle and the radiation frequencies corresponding to $γ -$ decays in the figure given below. (rest mass of au -198.968233 u and r.m. of Hg=198=197.966760 u)

Text Solution

Verified by Experts

Energies of $γ$ - photons $γ_{1}, γ_{2}, γ_{3}$ are
$E_{1} = (1.088 - 0) M e V = 1.088 M e V = 1.088 \times 1.6 \times 10^{- 13} = 1.7408 \times 10^{- 13} J$
$E_{2} = (0.412 - 0) M e V = 0.412 M e V = 0.412 M e V = 0.412 \times 1.6 \times 10^{- 13} = 0.6592 \times 10^{- 13} J$
$E_{3} = (1.088 - 0.452) M e V = 0.676 M e V = 0.672 \times 1.6 \times 10^{- 13} = 1.0816 \times 10^{- 13} J$
but frequency of radiation $v = \frac{E}{h}$

$∴ v_{1} = \frac{1.7408 \times 10^{- 13}}{6.625 \times 10^{- 34}} = 0.2628 \times 10^{21} H z = 2.628 \times 10^{24} H z$
$v_{2} = \frac{0.6592 \times 10^{- 13}}{6.625 \times 10^{- 34}} = 0.0955 \times 10^{21} H z = 9.55 \times 10^{19} H z$
$v_{3} = \frac{1.0816 \times 10^{- 13}}{6.625 \times 10^{- 34}} = 0.1633 \times 10^{21} H z = 1.633 \times^{20} H z$
$β_{1}^{-}$ decay, $_{(79)}^{198} A u \to_{80}^{198} H g +_{- 1}^{0} e + Q_{2} ({¯ β}_{1}) + Q_{1} (γ_{1})$
The maximum kinetic energy of $β_{1}^{-} = [197.968233 - 197.966760] \times 931.5 M e V = 0.284 M e V$
$β_{2}^{-}$ decay, $_{(79)}^{198} A u \to_{80}^{198} H g +_{- 1}^{0} e + Q_{2} ({¯ β}_{2}) + Q_{2} (γ_{2})$
The maximum kinetic energy of $β_{2}^{-} = [197.96822233 - 197.966760] \times 931.5 M e V - 0.412 M e V = 0.96 M e V$

|

Updated on:21/07/2023

Class 12 PHYSICS NUCLEI

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The kinetic energy of $α$ -particle emitted in the $α$ -decay of $_{88} R a^{266}$ is [given, mass number of Ra = 222 u]
A $5.201$ Me V
B $3.301$ Me V
C $6.023$ Me V
D $4.871$ Me V

SUBHASH PUBLICATION-NUCLEI-NUMARICALS WITH SOLUTIONS

Home
Ask Doubt
Profile