Obtain the position of centre of mass of a thin rod of uniform density. Solution in Gujrati
Homogeneous body means a body with uniformly distributed mass.
Let us consider a thin rod, whose width and breadth (in case of cross-section of the rod is rectangular) or radius (In case of the cross section of the rod is cylindrical) is much smaller than its length.
Taking the origin to be at the geometric centre of the rod and X-axis to be along the length of the rod, for every element dm of the rod at there is an element of the same mass dm located at .

The net contribution of every such pair to the integral and hence the integral. itself in zero.
Centre of mass of rod,
but
where = mass per unit length =
where L = length of rod,
.
Hence, centre of mass of thin rod of uniform density lies at midpoint of the length of rod means at its geometric centre.
Centre of mass of homogeneous ring, disc and spheres can be found in this way and above all bodies their centre of mass coincide with their geometric centre.
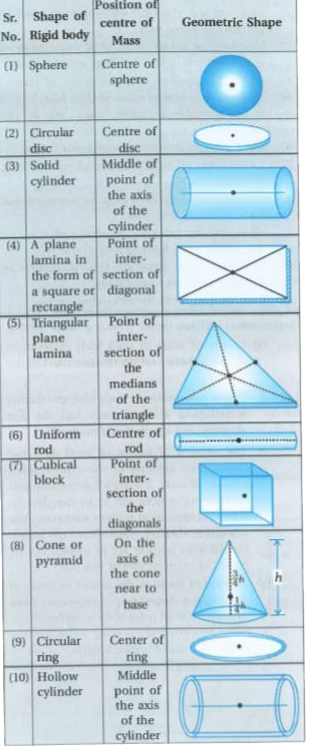
Position of centre of mass of bodies of regular shape :
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-A HOTS
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-A (TRY YOURSELF (VSQs))
94 Videos
- QUESTIONS ASKED IN JEE - 2020 BOOK - KUMAR PRAKASHANCHAPTER - QUESTIONS ASKED IN JEE - 2020 EXERCISE - Question
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
1 Videos
Similar Questions
What is torque? Explain the torque acting on a particle.
View SolutionWhat is a rigid body ? Explain the differences between rigid body and solid body.
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionCentre Of Mass Of Uniform Rod
View SolutionA uniform straight rod is placed in vertical position on a smooth horizontal surface and released. As the rod is in motion, the centre of mass moves
View SolutionA uniform thin rod of length 1m and mass 3kg is attached to a uniform thin circular disc of radius 30cm and mass 1kg at its centre perpendicular to its plane. The centre of mass of the combination from the centre of disc is
View SolutionA uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y- coordinate of the centre of mass of the system is
View SolutionCalculate Centre of mass of a non-uniform rod with linear mass density γ

λ(mass/length)=kx2
View SolutionFind out the position vector of centre of mass of the trapezium made out of uniform thin rods of same material.
View SolutionThe position of the centre of mass of a cube of uniform mass density will be at
View Solutionएकसमान पतली छड़ का द्रव्यमान केन्द्र कहाँ होता है ?
View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is lambda=lambda_(0)x . The distance of centre of mass of rod from the origin is :
View Solutionएक समान पतली छड़ के द्रव्यमान केन्द्र की स्थिति लिखिए।
View SolutionFind out the location of centre of mass of a uniform rod.

View Solution
