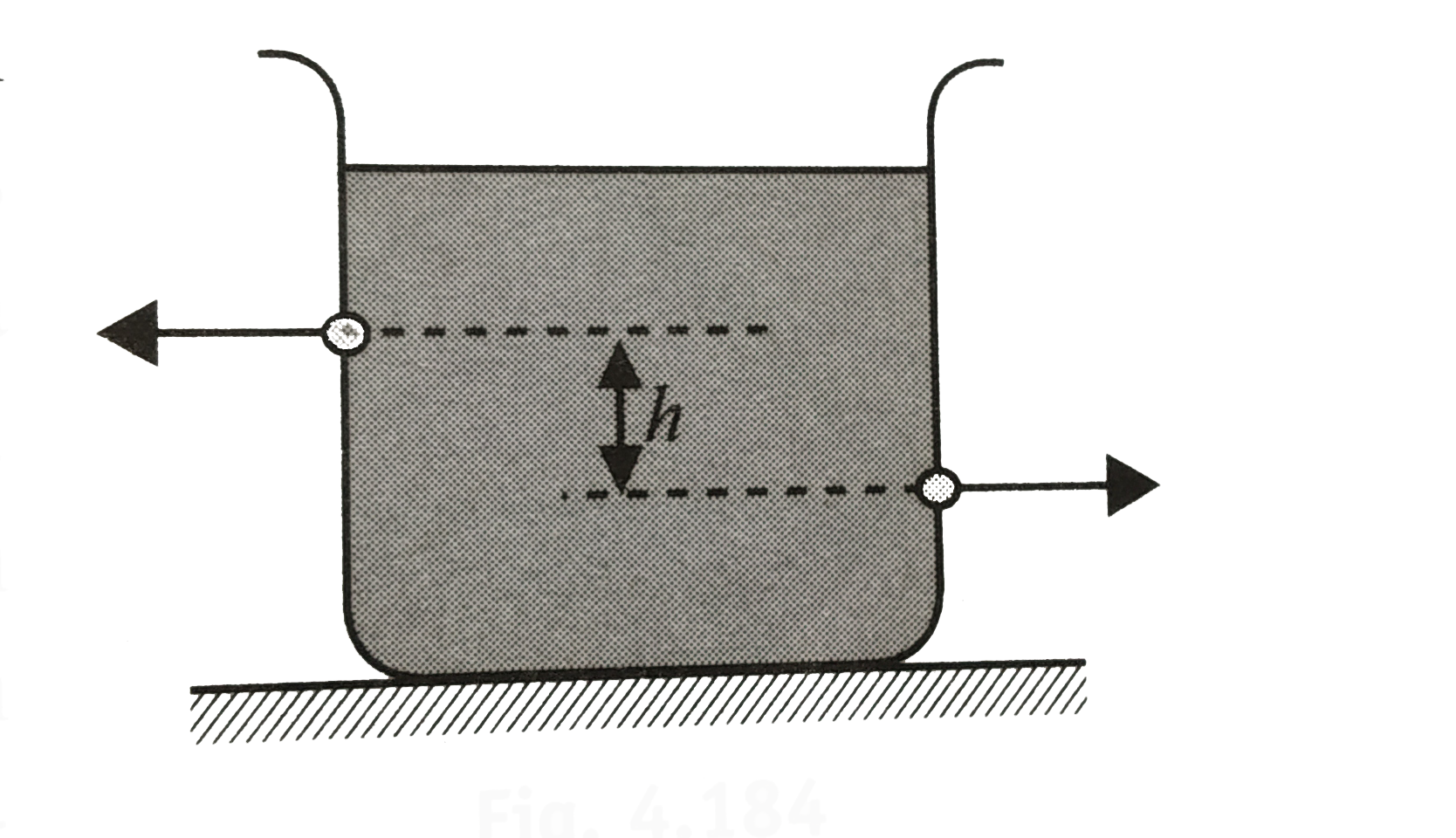
On the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
apgh/2
3apgh
apgh
2apgh
To solve the problem, we need to calculate the force exerted on the vessel due to the water flowing out of the two holes. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a vertical vessel filled with water, and two identical holes are opened on opposite sides of the vessel. The area of cross-section of each hole is A, and the difference in height of the water levels on either side of the vessel is h. The density of water is ρ.
Step 2: Determine the Efflux Speeds
Using Torricelli's theorem, the speed of efflux for each hole can be determined by the formula:
v=√2gh
where h is the height of the water column above the hole. For the two holes, we denote the heights as h1 and h2, where h2−h1=h.
Thus, the efflux speeds are:
v1=√2gh1andv2=√2gh2
Step 3: Calculate the Mass Flow Rate
The mass flow rate (dmdt) for each hole can be expressed as:
dmdt=ρAv
For hole 1:
dm1dt=ρAv1=ρA√2gh1
For hole 2:
dm2dt=ρAv2=ρA√2gh2
Step 4: Calculate the Forces on the Vessel
The force exerted on the vessel due to the water flowing out of each hole can be calculated using the change in momentum principle:
F=dmdt⋅v
For hole 1:
F1=dm1dt⋅v1=ρA√2gh1⋅√2gh1=ρA(2gh1)
For hole 2:
F2=dm2dt⋅v2=ρA√2gh2⋅√2gh2=ρA(2gh2)
Step 5: Calculate the Net Force on the Vessel
The net force acting on the vessel is the difference between the forces from the two holes:
Fnet=F2−F1=ρA(2gh2)−ρA(2gh1)
This simplifies to:
Fnet=ρA⋅2g(h2−h1)=2ρAgh
Final Answer
Thus, the force on the vessel is:
F=2ρAgh
We have a vertical vessel filled with water, and two identical holes are opened on opposite sides of the vessel. The area of cross-section of each hole is A, and the difference in height of the water levels on either side of the vessel is h. The density of water is ρ.
Using Torricelli's theorem, the speed of efflux for each hole can be determined by the formula:
v=√2gh
where h is the height of the water column above the hole. For the two holes, we denote the heights as h1 and h2, where h2−h1=h.
v1=√2gh1andv2=√2gh2
The mass flow rate (dmdt) for each hole can be expressed as:
dmdt=ρAv
For hole 1:
dm1dt=ρAv1=ρA√2gh1
For hole 2:
dm2dt=ρAv2=ρA√2gh2
The force exerted on the vessel due to the water flowing out of each hole can be calculated using the change in momentum principle:
F=dmdt⋅v
For hole 1:
F1=dm1dt⋅v1=ρA√2gh1⋅√2gh1=ρA(2gh1)
For hole 2:
F2=dm2dt⋅v2=ρA√2gh2⋅√2gh2=ρA(2gh2)
The net force acting on the vessel is the difference between the forces from the two holes:
Fnet=F2−F1=ρA(2gh2)−ρA(2gh1)
This simplifies to:
Fnet=ρA⋅2g(h2−h1)=2ρAgh
Thus, the force on the vessel is:
F=2ρAgh
Topper's Solved these Questions
Similar Questions
On the opposite sides of a wide vertical vessel filled with water, two identical holes are opened, each having cross sectiona area a. The height dference between them is equal to h. Find the resultant force of reaction of water flowing out of vessel.
View SolutionThere are two holes one each along the opposite sides of a wide rectangular tank. The cross section of each hole is 0.01m2 and the vertical distance between the holes is one meter. The tank is filled with water. The net force on the tank in newton when water flows out of the holes is (density of water 1000kg/m3)
View SolutionThe water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionThere are two identical small holes of area of cross section a on the opposite sides of a tank containing liquid of density ρ. The differences in height between the holes is h. The tank is resting ona smooth horizontal surface. The horizontal force which will have to be applied on the tank to keep it inequilibrium is
 View Solution
View SolutionA closed vessel is half filled with water. There is a hole near the top of vessel and air is pumped out from this hole.
View SolutionCurved surface of a vessel has shape of truncated cone having semi-vertex angle 37∘. Vessel is full of water (density ρ=1000kg/m3) upto a height of 13cm and is placed on a smooth horizontal plane. Upper surface is opened to atmosphere. A hole of 1.5cm is made on curved wall of a height of 8cm from bottom as shown in figure. Area of water surface in the vessel is large as compared to the area of the hole.

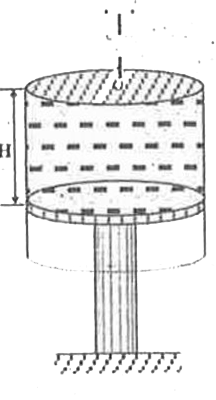
The initial horizontal range of water from point B isView SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is
 View Solution
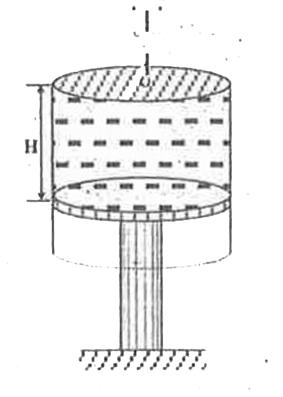
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H ).Find the speed of the vessel with which it move
 View Solution
View SolutionA fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
View SolutionThe figures given below are cross-sections of blood vessels
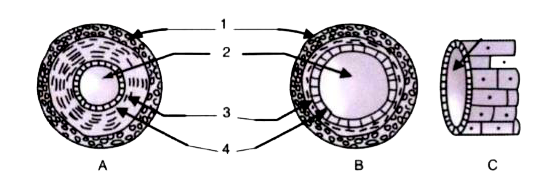
Venlion two structural differences between A and bView Solution

