Path of a particle moving in x−y plane is y=3x+4. At some instant suppose x- component of velocity is 1m/s and it is increasing at a constant rate of 1m/s2. Then at this instant.
(a)speed of particle is √10m/s
(b)acceleration of particle is √10m/s
(c)velocity time graph is parabola
(d)acceleration time graph is parabola
The correct Answer is:A, B
To solve the problem step by step, we will analyze the motion of a particle in the x-y plane given the equation of its path and the conditions of its velocity and acceleration.
Step 1: Understand the path of the particle
The path of the particle is given by the equation:
y=3x+4
This is a linear equation, which represents a straight line in the x-y plane.
Step 2: Determine the slope of the path
The slope of the line can be determined from the equation. The slope (m) is 3, which means for every unit increase in x, y increases by 3 units.
Step 3: Find the angle of inclination
The angle θ that the line makes with the x-axis can be found using the tangent of the angle:
tan(θ)=slope=3
Thus,
θ=tan−1(3)
Step 4: Analyze the velocity components
At the given instant, the x-component of velocity vx is:
vx=1m/s
It is also given that vx is increasing at a constant rate of:
ax=1m/s2
Step 5: Relate the y-component of velocity
Since the particle is moving along the path y=3x+4, we can find the y-component of the velocity vy using the relationship between the components of velocity and the slope of the path:
vyvx=slope=3
Thus,
vy=3vx=3×1=3m/s
Step 6: Find the total velocity
The total velocity v can be calculated using the Pythagorean theorem:
v=√v2x+v2y=√(1)2+(3)2=√1+9=√10m/s
Step 7: Analyze the acceleration components
The acceleration in the y-direction ay can be found using the same slope relationship:
ayax=slope=3
Thus,
ay=3ax=3×1=3m/s2
Step 8: Summary of results
At the instant described:
- The x-component of velocity vx=1m/s
- The y-component of velocity vy=3m/s
- The total velocity v=√10m/s
- The x-component of acceleration ax=1m/s2
- The y-component of acceleration ay=3m/s2
The path of the particle is given by the equation:
y=3x+4
This is a linear equation, which represents a straight line in the x-y plane.
The slope of the line can be determined from the equation. The slope (m) is 3, which means for every unit increase in x, y increases by 3 units.
The angle θ that the line makes with the x-axis can be found using the tangent of the angle:
tan(θ)=slope=3
Thus,
θ=tan−1(3)
At the given instant, the x-component of velocity vx is:
vx=1m/s
It is also given that vx is increasing at a constant rate of:
ax=1m/s2
Since the particle is moving along the path y=3x+4, we can find the y-component of the velocity vy using the relationship between the components of velocity and the slope of the path:
vyvx=slope=3
Thus,
vy=3vx=3×1=3m/s
The total velocity v can be calculated using the Pythagorean theorem:
v=√v2x+v2y=√(1)2+(3)2=√1+9=√10m/s
The acceleration in the y-direction ay can be found using the same slope relationship:
ayax=slope=3
Thus,
ay=3ax=3×1=3m/s2
At the instant described:
- The x-component of velocity vx=1m/s
- The y-component of velocity vy=3m/s
- The total velocity v=√10m/s
- The x-component of acceleration ax=1m/s2
- The y-component of acceleration ay=3m/s2
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MATCH THE COLUMN
10 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
y component of velocity is 20andx component of velocity is 10. The direction of motion of the body with the horizonatal at this instant is
View SolutionA particle is moving in x-y plane. At an instant, it has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2 At that instant, the radius of curvature of its path will be :
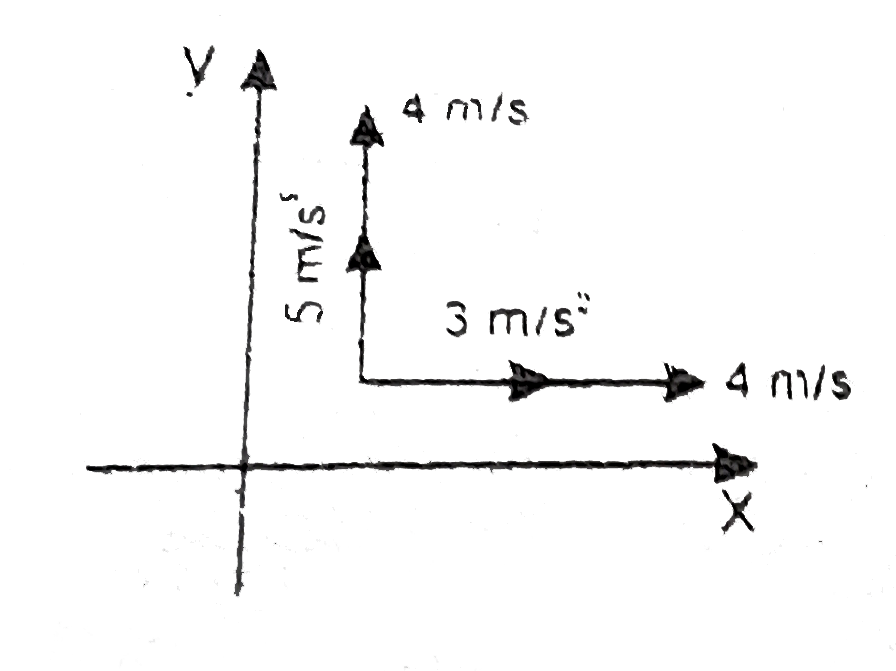
View Solution
Knowledge Check
A particle is moving on a circular path of 10 m radius. At any instant of time, its speed is 5ms−1 and the speed is increasing at a rate of 2ms−2. At this instant, the magnitude of the net acceleration will be
A5ms−2B2ms−2C3.2ms−2D4.3ms−2
x and y co-ordinates of a particle moving in x−y plane at some instant of time are x=2t and y=4t.Here x and y are in metre and t in second. Then
The distance travelled by the particle in a time from t=0 to t=2s is ………m
View SolutionA vehicle is moving at a speed of 30 m/s on a circular road of radius 450 m. Its speed is increasing at a rate of 2ms2 . The acceleration of particle at this instant is
View Solutionx and y co-ordinates of a particle moving in x−y plane at some instant of time are x=2t and y=4t.Here x and y are in metre and t in second. Then
The path of the particle is a…….
View SolutionA particle of mass m moves along a curve y=x2. When particle has x-coordinate as 12 m and x-component of velocity as 4ms, then
View SolutionA person drops a stone from a building of height 20 m. At the same instant the front end of a truck passes below the building moving with constant acceleration of 1m/s2 and velocity of 2m/s at that instant. Length of the truck if the stone just misses to hit its rear part is :-
View SolutionA particle is moving in the x-y plane. At certain instant of time, the components of its velocity and acceleration are as follows: vx=3ms−1,vy=4ms−1,ax=2ms−2anday=1ms−2. The rate of change of speed at this moment is
View SolutionA particle is moving on a circular path of radius 1 m with 2 m/s. If speed starts increasing at a rate of 2m/s2, then acceleration of particle is
View Solution
