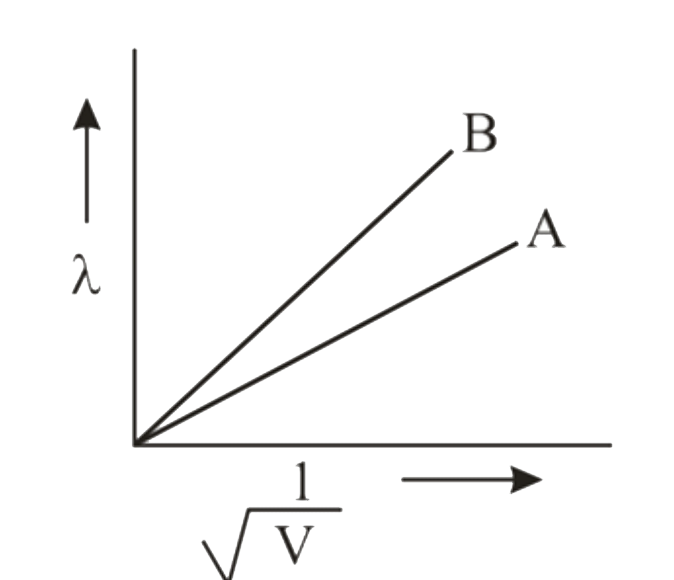
Plot a graph showing variation of de-broglie wavelength λ versus 1/√V, where V is accelerating potential for two particle A and P carrying same charge but of masses m1andm2(m1>m2). Which one of the two represents a particle of smaller mass and why?
To solve the problem of plotting the graph of de Broglie wavelength (λ) versus 1√V for two particles A and P with different masses, we will follow these steps:
1. Understanding the de Broglie Wavelength Formula:
The de Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where p is the momentum of the particle. For a charged particle accelerated through a potential V, the momentum can be expressed in terms of mass m and the charge Q:
p=√2mQV
Therefore, substituting this into the de Broglie wavelength formula gives:
λ=h√2mQV
2. Rearranging the Formula:
We can express λ in terms of 1√V:
λ=h√2mQ⋅1√V
This shows that λ is inversely proportional to √V.
3. Identifying the Relationship:
From the equation λ=h√2mQ⋅1√V, we can see that:
- The slope of the graph when plotting λ versus 1√V is given by h√2mQ.
- This means that the slope depends on the mass of the particle.
4. Comparing Two Particles:
Let’s denote the masses of the two particles as m1 for particle A and m2 for particle P, where m1>m2:
- For particle A (mass m1), the slope will be h√2m1Q.
- For particle P (mass m2), the slope will be h√2m2Q.
5. Analyzing the Slopes:
Since m1>m2, it follows that:
√m1>√m2⟹1√m1<1√m2
Therefore, the slope for particle P (smaller mass) will be greater than that for particle A (larger mass).
6. Plotting the Graph:
- On the x-axis, plot 1√V.
- On the y-axis, plot λ.
- The graph will show two lines: one for particle A and one for particle P. The line for particle P will have a steeper slope than that for particle A.
7. Conclusion:
The particle with the smaller mass (particle P) will have a greater slope in the graph of λ versus 1√V.
Final Graph:
- The graph will be a straight line for each particle, with the line for particle P being steeper than that for particle A.
The de Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where p is the momentum of the particle. For a charged particle accelerated through a potential V, the momentum can be expressed in terms of mass m and the charge Q:
p=√2mQV
Therefore, substituting this into the de Broglie wavelength formula gives:
λ=h√2mQV
We can express λ in terms of 1√V:
λ=h√2mQ⋅1√V
This shows that λ is inversely proportional to √V.
From the equation λ=h√2mQ⋅1√V, we can see that:
- The slope of the graph when plotting λ versus 1√V is given by h√2mQ.
- This means that the slope depends on the mass of the particle.
Let’s denote the masses of the two particles as m1 for particle A and m2 for particle P, where m1>m2:
- For particle A (mass m1), the slope will be h√2m1Q.
- For particle P (mass m2), the slope will be h√2m2Q.
Since m1>m2, it follows that:
√m1>√m2⟹1√m1<1√m2
Therefore, the slope for particle P (smaller mass) will be greater than that for particle A (larger mass).
- On the x-axis, plot 1√V.
- On the y-axis, plot λ.
- The graph will show two lines: one for particle A and one for particle P. The line for particle P will have a steeper slope than that for particle A.
The particle with the smaller mass (particle P) will have a greater slope in the graph of λ versus 1√V.
- The graph will be a straight line for each particle, with the line for particle P being steeper than that for particle A.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - NCERT Exerciese question
1 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Short answer
1 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Problems for Practice (B)
2 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Multiple Choice Questions
1 Videos
Similar Questions
Plot a graph showing variation of de-broglie wavelength λ versus 1/√V, where V is accelerating potential for two particle A and P carrying same charge but of masses m1andm2(m1>m2). Which one of the two represents a particle of smaller mass and why?
View SolutionTwo lines, A and B, in the plot given below show the variation of de-Broglie wavelength, λ versus 1/√V, where V is the accelerating potential difference, for two particles carrying the same charge. Which one of two represents a particle of smaller mass?
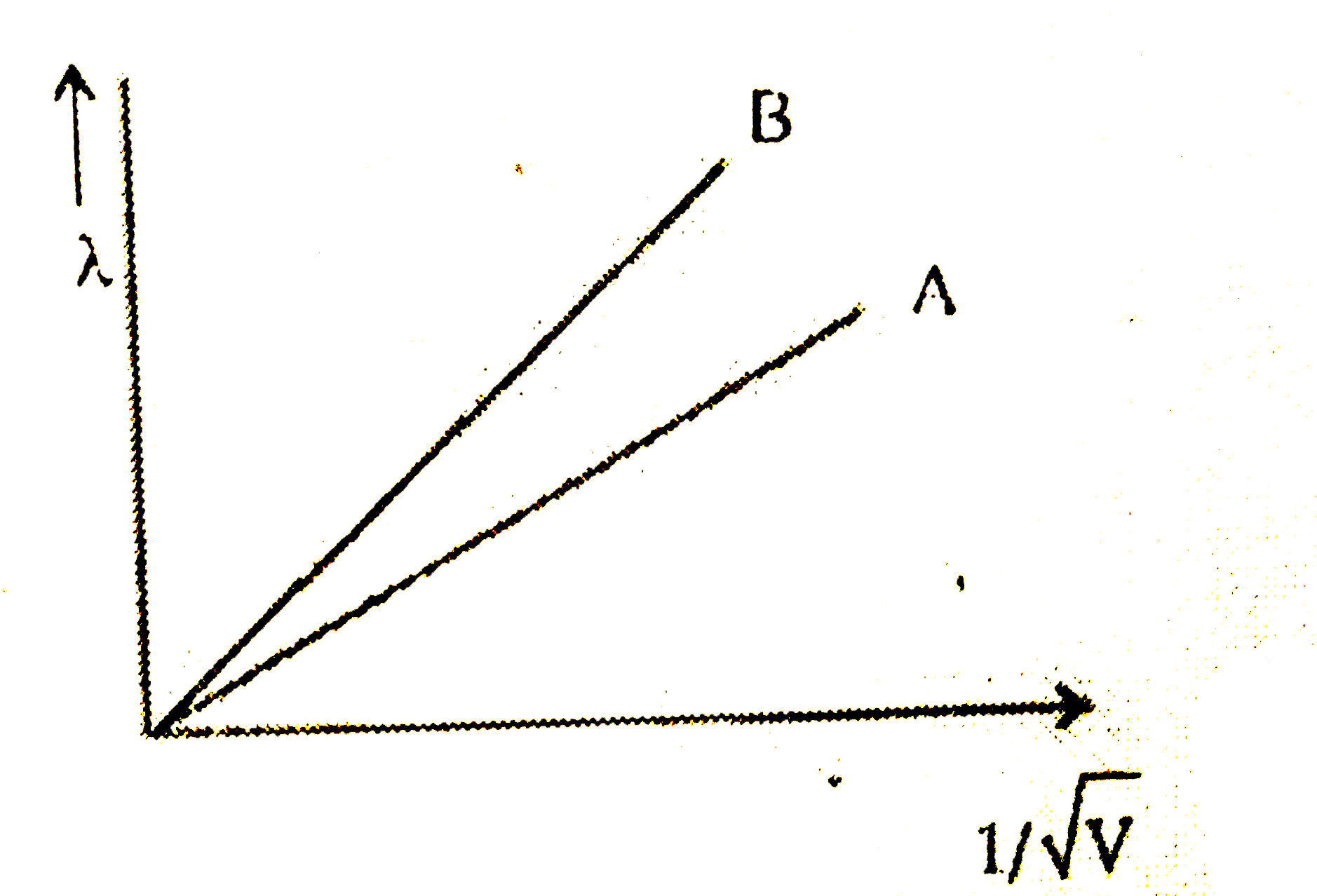
View Solution
Knowledge Check
Two particles A1andB2 of masses m1andm2(m1>m2) have the same de Broglie wavelength . Then
Atheir momenta are the same.Btheir energies are the sameCthe energy of A1 is less than the energy of A2Dthe energy of A1 is more than the energy of A2Which of the following graphs shows the variation of de-Broglie wavelength with potential through which a particle of charge q and mass m is accelerated ?
A B
B C
C D
D
de Broglie wavelengths of two particles A and B are plotted against (1√V) , where V is the potential on the particles. Which of the following relation is correct about the mass of the particles ?
 AmA=mBBmA>mBCmA<mBDmA≤mB
AmA=mBBmA>mBCmA<mBDmA≤mB

The two lines A and B in fig. shoe the phot of de Broglie wavelength (λ) as a function of 1√V(V is the accelerating potential) for teo particles having the same charge. Which of the two represents the particle of heavier mass?
View SolutionPlot a graph showing variation of a de Broglie wavelength (λ) associated with a charged particle of mass m, verses 1/√V, where V is the potential difference thrugh which the particle is accelerated. How does this graph give us the information the magnitude the magnitude of the charge of the particle ?
View SolutionDraw a graph showing the variation of de Broglie wavelength of a particle of charge q and mass m with accelerating potential. Proton and deuteron have the same de Broglie wavelengths. Explain which has more kinetic energy.
View Solution(a) Draw a graph showing the variation of de-Broglie wavelength of a particle of charge 'q' and mass 'm' with accelerating potential 'V'.
(b) Proton and deuteron have the same de-Broglie wavelength. Explain which has more kinetic enegy.
View SolutionThe de-Broglie wavelength λ associated with charged particle of charge q, mass m and potential difference V is
View Solution
