Refer to the collision of two blocks on a frictionless table. Before the collision, the block of mass m iss at rest.
Q. What is the total momentum of the blocks just AFTER THE COLLISION?
12kg⋅m/s
16kg⋅m/s
18kg⋅m/s
32kg⋅m/s
The correct Answer is:D
Using the equation P=mv, we can figure out that before the collision, the momentum of the left-hand block was (4kg) (8 m/s)=32kg.m/s, and that of the righ-hand block was zero (since it was at rest), so the total momentum before the collision was 32 kg⋅m/s. since total momentum is conserved in the collision, the total momentum after the collision must also be 32 kg⋅m/s.
Topper's Solved these Questions
Similar Questions
A block of mass 3M connected to a massless rod of length L lies at rest on a fixed frictionless table. A second block of mass M moving with speed v0 strikes the opposite end of the rod at right angle and sticks. The velocity of centre of mass of the system after collision is
_PHY_E05_239_Q01.png)
View SolutionA block of mass M=4kg is moving with velocity V=6m/s toward a target block of mass=2kg, which is stationary (v=0). The object collide heat-on, and immediately after the collision, the speed of block m is 4 times the speed of block M.
Q. What is the speed of block M after the collision?
View Solution
Knowledge Check
The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is
AkL22MB√MkL(c)SCML2kDzeroThe collision between both blocks shown in figure is completely inelastic. The total energy of oscillation after collision is
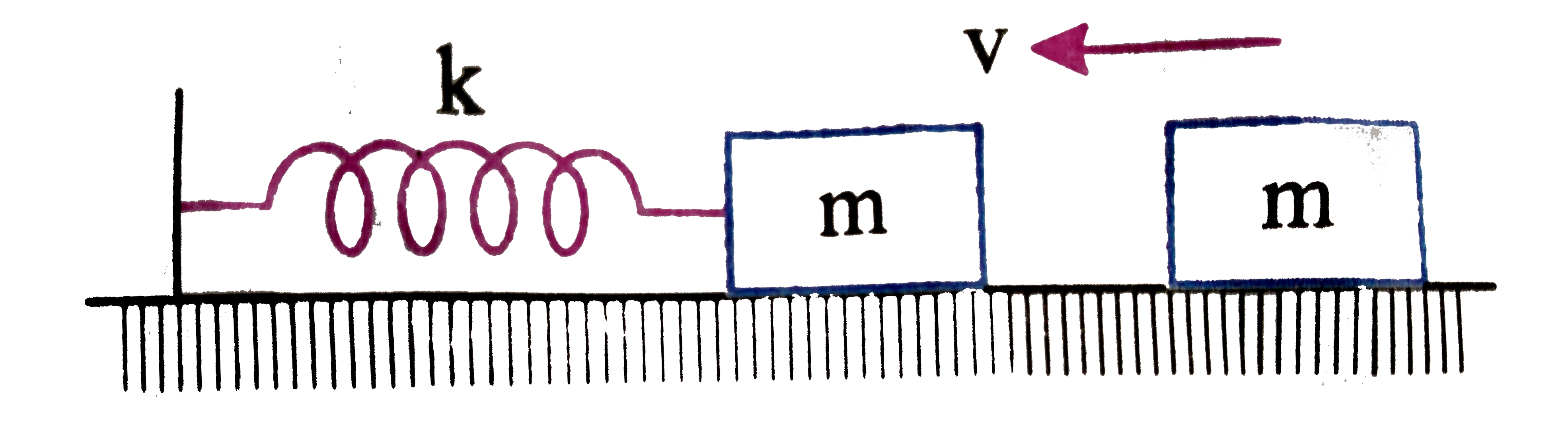A12mv2Bmv28Cmv24Dmv232
The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is
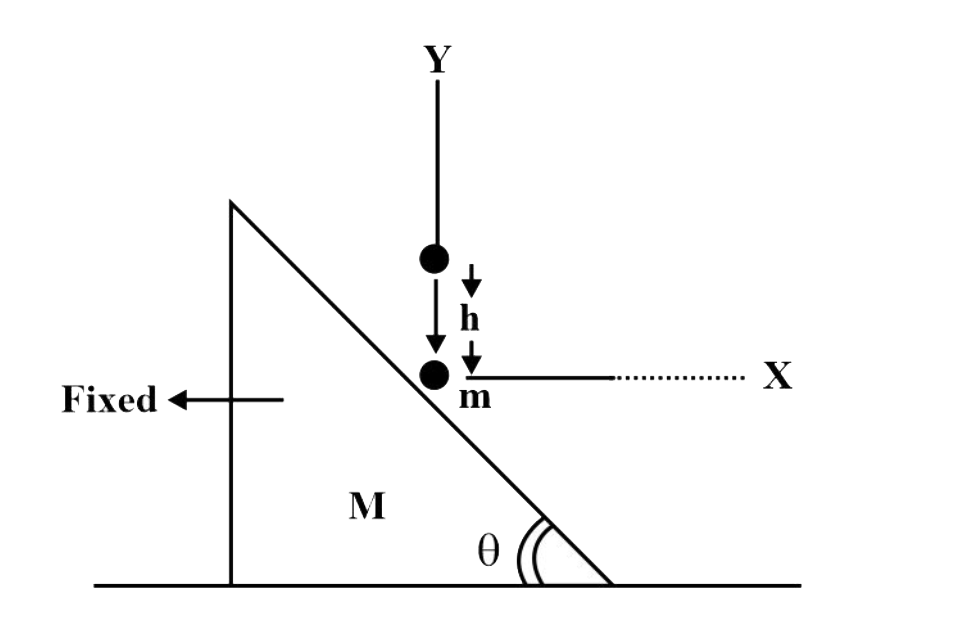
View SolutionA ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is component of the velocity of the block is √2gh , then θ is
View SolutionA steel ball weighting 1 kg is fastened to a cord 1 m long and is released when the cord is horizontal . At the bottom of its path the ball strikes a 5-kg steel block initially at rest on a frictionless surface . The collision is elastic . Find the speed of the ball and speed of the block just after collision . (g = 9.8ms−2)
[Hint : Apply principal of conservation of momentum and conservation of kinetic energy as the collision is elastic .]
View SolutionA block of mass m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of the blocks after the collision.
View SolutionA block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionA block of mass m moving at speed υ collides wilth another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View Solution