Show on a diagram the vector that would represent the angular velocity of the earth rotating about its axis.
To show the vector that represents the angular velocity of the Earth rotating about its axis, we can follow these steps:
Step 1: Draw the Earth
- Begin by sketching a circle to represent the Earth. Label the top of the circle as the North Pole and the bottom as the South Pole.
Step 2: Indicate the Axis of Rotation
- Draw a straight line vertically through the center of the circle to represent the axis of rotation. This line should extend above the North Pole and below the South Pole.
Step 3: Show the Direction of Rotation
- From the North Pole perspective, indicate the direction of rotation. Since the Earth rotates counterclockwise when viewed from above the North Pole, draw an arrow along the edge of the circle in a counterclockwise direction.
Step 4: Apply the Right-Hand Rule
- To determine the direction of the angular velocity vector (ω), use the right-hand rule:
- Curl the fingers of your right hand in the direction of the Earth's rotation (counterclockwise).
- Your thumb will point upwards, indicating the direction of the angular velocity vector.
Step 5: Draw the Angular Velocity Vector
- Draw a vector (an arrow) starting from the center of the Earth (the axis of rotation) pointing upwards, indicating the direction of the angular velocity vector. Label this vector as ω.
Final Diagram
- Your final diagram should clearly show the Earth, the axis of rotation, the direction of rotation, and the angular velocity vector pointing upwards.
- Begin by sketching a circle to represent the Earth. Label the top of the circle as the North Pole and the bottom as the South Pole.
- Draw a straight line vertically through the center of the circle to represent the axis of rotation. This line should extend above the North Pole and below the South Pole.
- From the North Pole perspective, indicate the direction of rotation. Since the Earth rotates counterclockwise when viewed from above the North Pole, draw an arrow along the edge of the circle in a counterclockwise direction.
- To determine the direction of the angular velocity vector (ω), use the right-hand rule:
- Curl the fingers of your right hand in the direction of the Earth's rotation (counterclockwise).
- Your thumb will point upwards, indicating the direction of the angular velocity vector.
- Draw a vector (an arrow) starting from the center of the Earth (the axis of rotation) pointing upwards, indicating the direction of the angular velocity vector. Label this vector as ω.
- Your final diagram should clearly show the Earth, the axis of rotation, the direction of rotation, and the angular velocity vector pointing upwards.
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (VERY SHORT ANSWER QUESTIONS)
14 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM EQUATIONS OF ROTATIONAL MOTION)
8 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (LONG ANSWER QUESTIONS)
14 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
Knowledge Check
The angular speed of rotation of the earth is
A7.3×10−5rads−1B7.3×10−4rads−1C7.3×10−6rads−1D7.3×10−3rads−1
What is the angular velocity of a particle lying on the axis of rotation ?
View SolutionThe angular speed of earth around its own axis is
View SolutionA satellite can be in a geostationary orbit around earth in an orbit of radius r. If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit aroun earth radius
View SolutionA satellite can be in a geostationary orbit around earth in an orbit of radius r. If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit aroun earth radius
View SolutionWhich is greater , the angular velocity of the hour hand of a watch or angular velocity of earth around its own axis ?
View SolutionA copper ball of mass m=1kg with a radius of r=10cm rotates with angular velocity ω=2rad/s about an axis passing through its centre. The work should be performed to increase the angular velocity of rotation of the ball two fold is.
View SolutionA particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle θ from the axis.
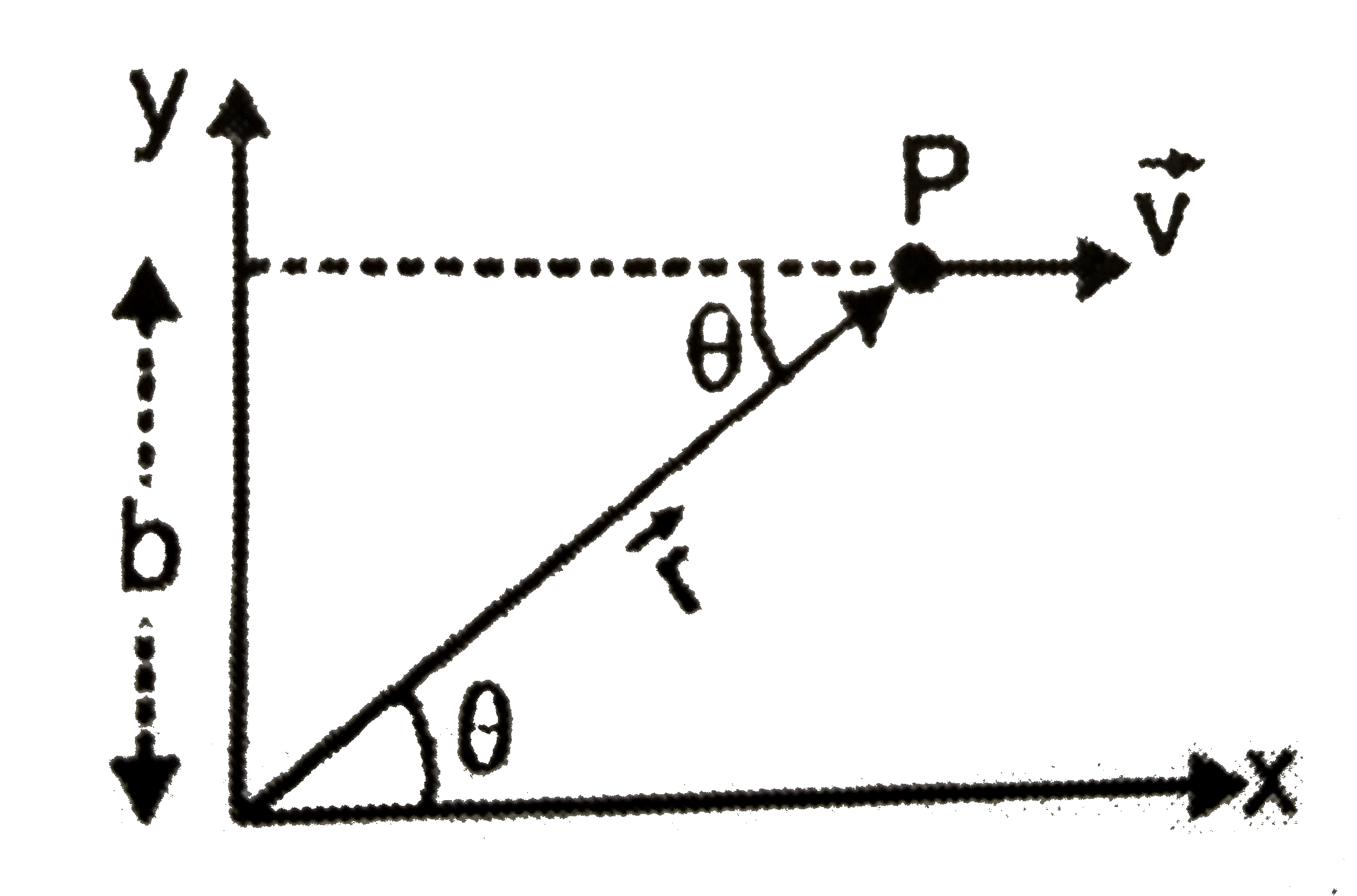
View Solution