A particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle θ from the axis.
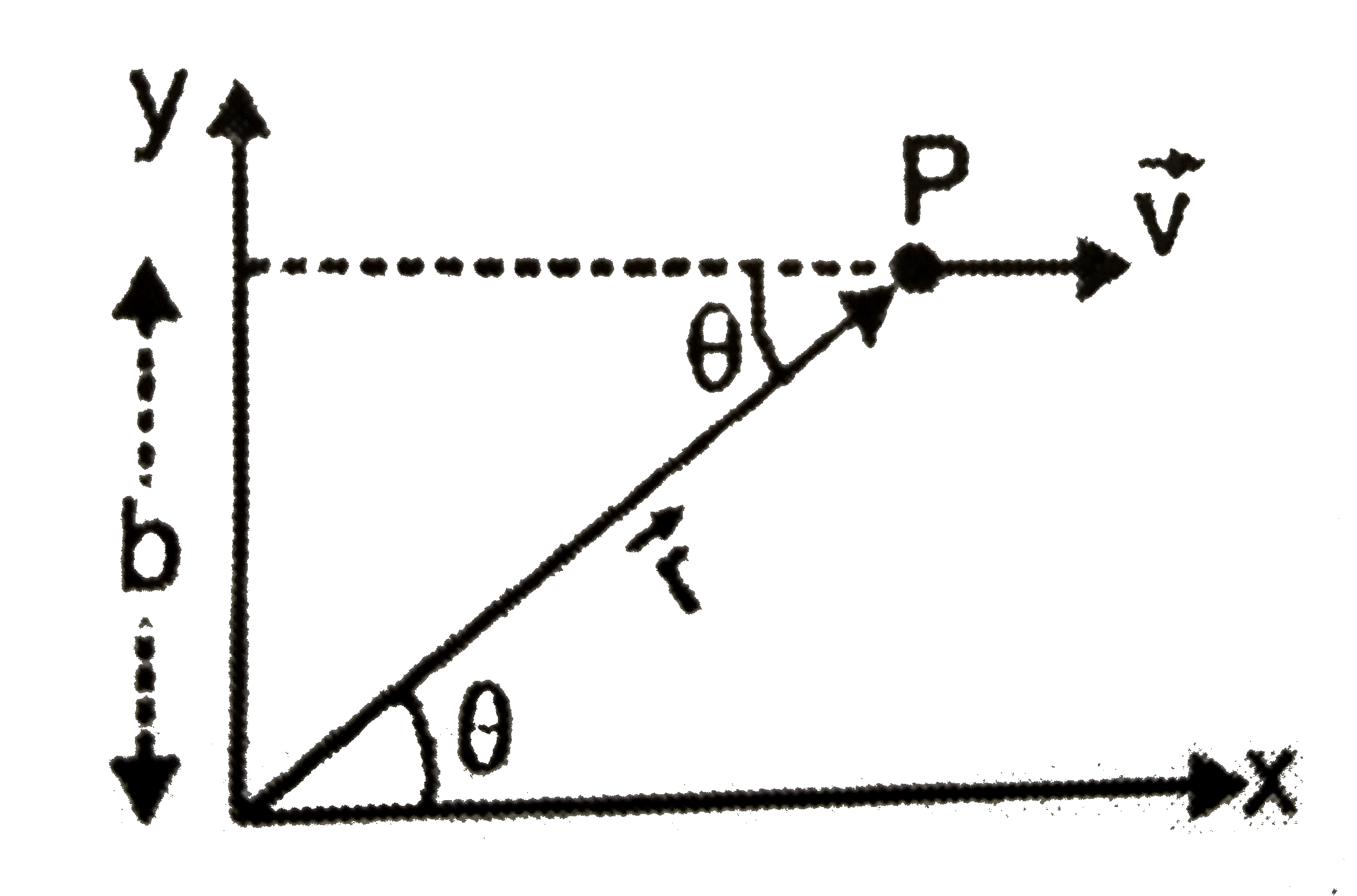
?XP/O=vsin0=vbsin20
bsin0

Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - SOLVED EXAMPLES20videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - PRACTICE EXERCISE80videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE52videos
MOTION IN A STRAIGHT LINE & PLANE
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ2videos
Motion in Two Dimensions
Similar Questions
A particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
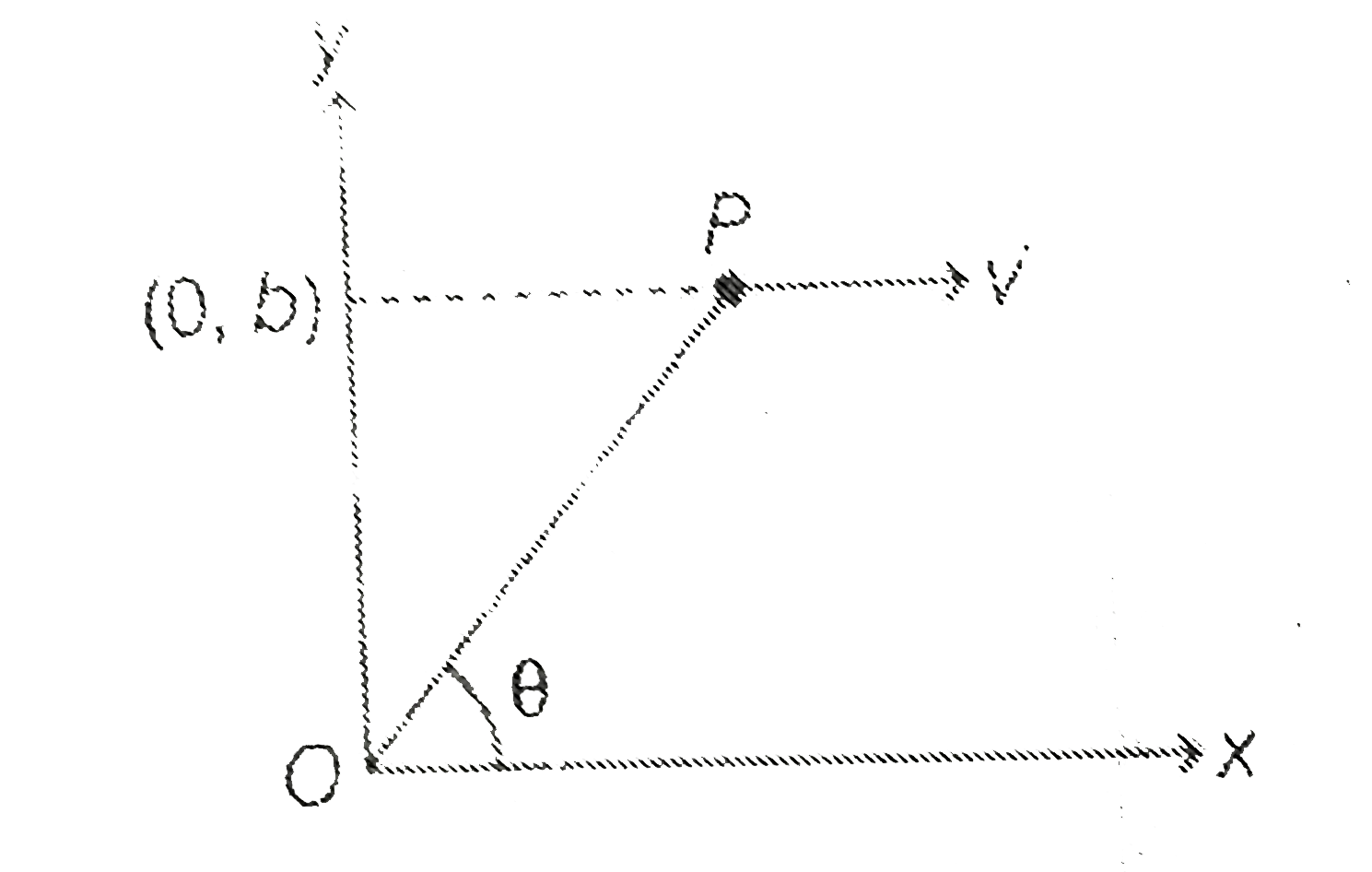 View Solution
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionShow on a diagram the vector that would represent the angular velocity of the earth rotating about its axis.
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :
 View Solution
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
 View Solution
View SolutionA particle moves in space such that its position vector varies as →r=2tˆi+3t2ˆj. If mass of particle is 2 kg then angular momentum of particle about origin at t=2 sec is
View SolutionA particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
View Solution

