Show that moment of inertia of a solid body of any shape changes with temperature as I=I0(1+2αθ). Where I0 is the moment of inertia at 0∘C and α is the coefficient of linear expansion of the solid.
To show that the moment of inertia of a solid body of any shape changes with temperature as I=I0(1+2αθ), where I0 is the moment of inertia at 0∘C and α is the coefficient of linear expansion of the solid, we can follow these steps:
Step 1: Define the Moment of Inertia at 0∘C
The moment of inertia I0 at 0∘C is defined as:
I0=∑mir2i
where mi is the mass of the ith particle and ri is its distance from the axis of rotation.
Step 2: Determine the Effect of Temperature on Distance
When the temperature increases from 0∘C to θ∘C, the distances ri change due to thermal expansion. The new distance r′i can be expressed as:
r′i=ri(1+αθ)
where α is the coefficient of linear expansion and θ is the change in temperature.
Step 3: Write the Moment of Inertia at Temperature θ
The moment of inertia at the new temperature θ becomes:
I=∑mi(r′i)2=∑mi(ri(1+αθ))2
Expanding this expression gives:
I=∑mir2i(1+αθ)2
Step 4: Expand the Squared Term
Now, we can expand (1+αθ)2:
(1+αθ)2=1+2αθ+α2θ2
Substituting this back into the moment of inertia equation, we have:
I=∑mir2i(1+2αθ+α2θ2)
Step 5: Simplify the Expression
Now, we can separate the terms:
I=∑mir2i+∑mir2i(2αθ)+∑mir2i(α2θ2)
Recognizing that ∑mir2i=I0, we get:
I=I0+2αθ∑mir2i+α2θ2∑mir2i
Since α2θ2 is a very small term (as α is small), we can neglect it:
I≈I0+2αθI0
Step 6: Factor Out I0
Factoring out I0 gives:
I≈I0(1+2αθ)
Conclusion
Thus, we have shown that the moment of inertia at temperature θ is given by:
I=I0(1+2αθ)
The moment of inertia I0 at 0∘C is defined as:
I0=∑mir2i
where mi is the mass of the ith particle and ri is its distance from the axis of rotation.
When the temperature increases from 0∘C to θ∘C, the distances ri change due to thermal expansion. The new distance r′i can be expressed as:
r′i=ri(1+αθ)
where α is the coefficient of linear expansion and θ is the change in temperature.
The moment of inertia at the new temperature θ becomes:
I=∑mi(r′i)2=∑mi(ri(1+αθ))2
Expanding this expression gives:
I=∑mir2i(1+αθ)2
Now, we can expand (1+αθ)2:
(1+αθ)2=1+2αθ+α2θ2
Substituting this back into the moment of inertia equation, we have:
I=∑mir2i(1+2αθ+α2θ2)
Now, we can separate the terms:
I=∑mir2i+∑mir2i(2αθ)+∑mir2i(α2θ2)
Recognizing that ∑mir2i=I0, we get:
I=I0+2αθ∑mir2i+α2θ2∑mir2i
Since α2θ2 is a very small term (as α is small), we can neglect it:
I≈I0+2αθI0
Factoring out I0 gives:
I≈I0(1+2αθ)
Thus, we have shown that the moment of inertia at temperature θ is given by:
I=I0(1+2αθ)
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Question for Shor Answer
13 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 1
12 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers
18 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
Similar Questions
If I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of I1 to I2 is
View SolutionThe volume of a solid decreases by 0.6% when it is cooled through 50∘C. Its coefficient of linear expansion is
View Solution
Knowledge Check
The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα
If I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View SolutionThe height of a mercury column measured with a brass scale, which is correct and equal to H0 at 0∘C, is H1 at t∘C? The coefficient of linear expansion of brass is α and the coefficient of linear expansion of brass is α and the corfficient of volume expansion of mercury is γ. Relate H0 and H1.
View SolutionFour solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of I0 & IA , where I0 is the moment of inertia of the system about an axis through the centre of the square and IA is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)
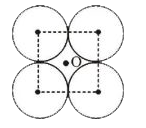
View SolutionFour solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of I0 & IA , where I0 is the moment of inertia of the system about an axis through the centre of the square and IA is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)

View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionWhen the temperature of a rod increases from t to r+Δt, its moment of inertia increases from I to I+ΔI. If α is the value of ΔI/I is
View SolutionCoefficient of areal expansion of a solid is 2×10−5.∘C−1. Calculate its coefficient of linear expansion.
View Solution
