shows a conducting disc rotating about its axis in a perpendicular magnetic field B. A resistor of resistance R is connected between the centre and the rim. Calculate the current in the resistor. Does it enter the disc or leave it at the centre? The radius of the disc is 5.0 cm , angular speed ω=10rads,B=0.40T and R=10Ω.

Here B=0.10T, omega=10 rad//s<br>R=10 Omega, r=5 cm=0.5m<br>Considering a rod rotating with the same omega,<br>theta =(1/2)xxomega=(0.05)/(2)xx10<br>theta =Blv<br>=0.40xx(0.05/2)xx10xx0.05<br>=5xx10^(-3)V.<br>i=R=(theta/R)<br>=(5xx10^(-3))/(10)=0.5 mA.<br>It leaves from the center..
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
Similar Questions
The following figure a conducting disc rotating about its axis in a perpendicular magnetic field B. The resistor of resistance R is connected between the centre and the rim. The current in the resistor is (The radius of the disc is 5.0 cn=m, angular speed ω=10rads−1,B=0.40TandR=10Ω)
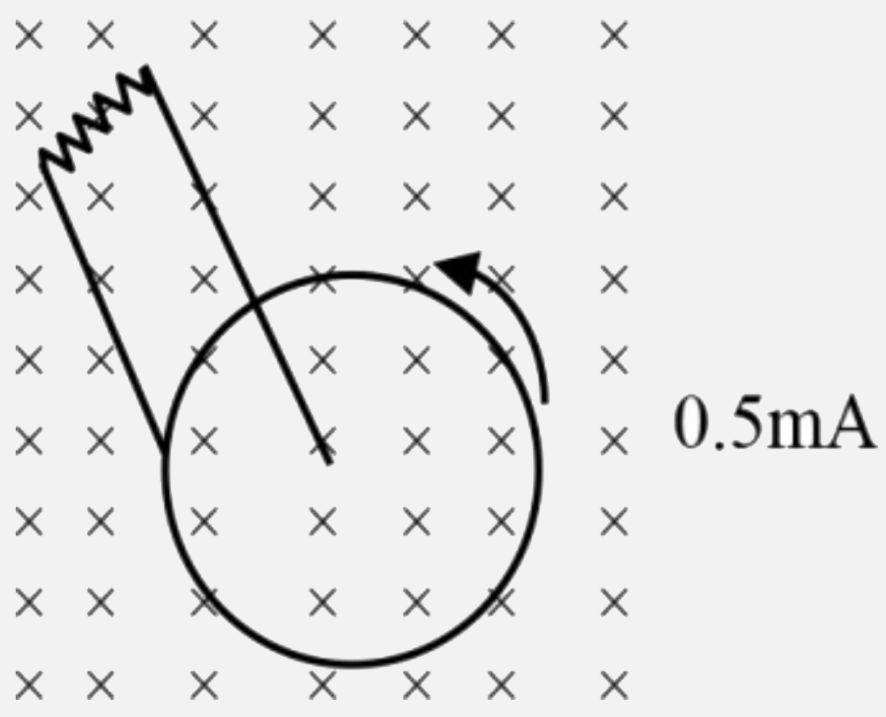 View Solution
View SolutionA copper disc of radius 10 cm rotates 20 times per scond with its axis parallel to a uniform magnetic field of 0.5 tesla . Calculate the induced emf between the centre and the edge of the disc.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows a conducting disc rotating about its axis in a perpendicular uniform and constant magnetic field B. A resistor of resistance R is connected between the centre and the rim. The radius of the disc is 5.0 cm, angular speed ω=40rad/s,B=0.10T and R=1Ω. The current through the resistor is
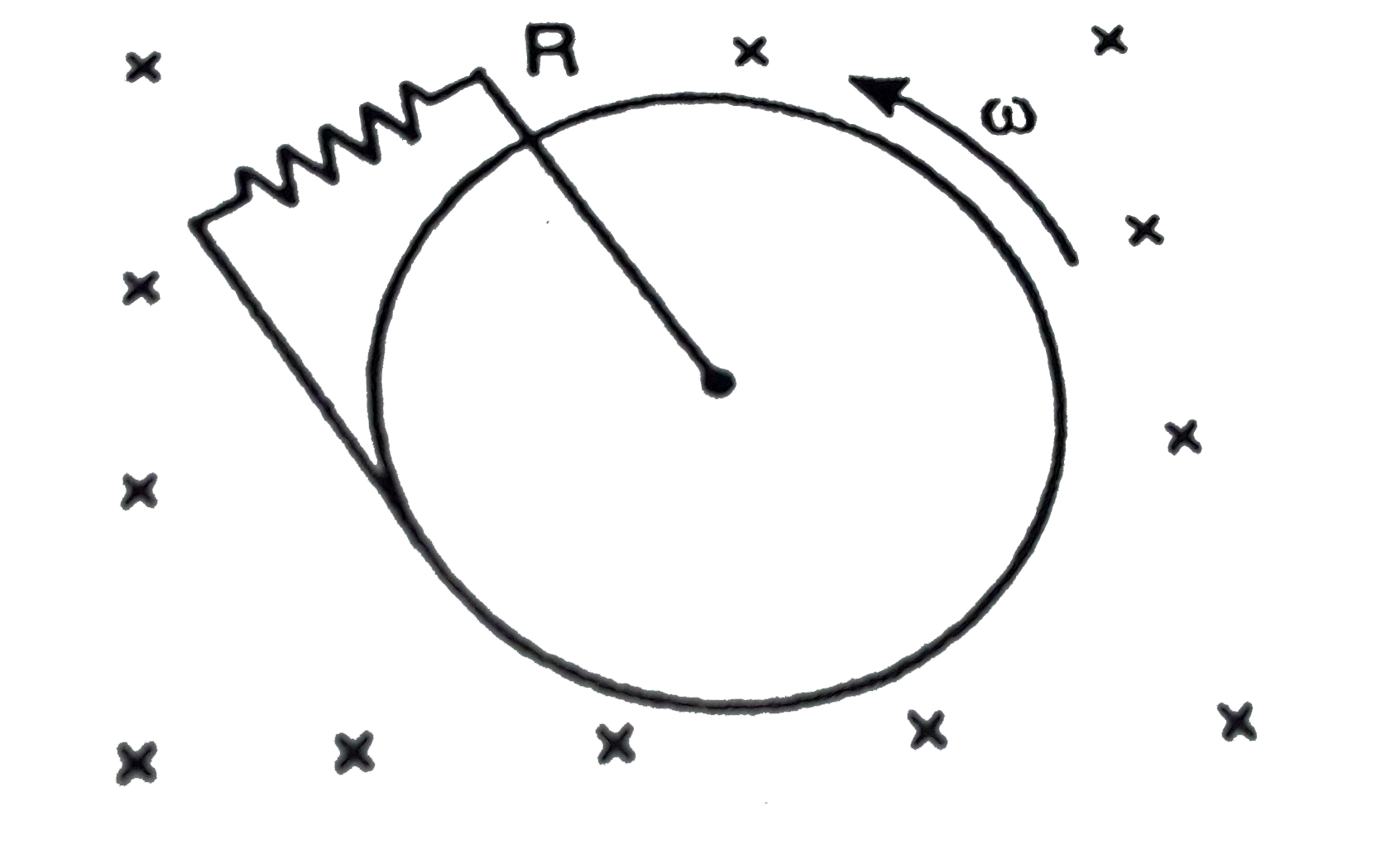 A5mAB50AC5AD10mA
A5mAB50AC5AD10mA - Question 2 - Select One
a conducting disc of radius R roatates about its axis when an angular velocity ω.Then the potential difference between the centre of the disc and its edge is (no magnetic field is present ):
AzeroBmeω2R22eCmeω2R23eDemeω2R22 - Question 3 - Select One
A non-conducting disk of radius R is rotating about its own axis with constant angular velocity ω in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
 ABωR22BBωR2CZeroDBωR23
ABωR22BBωR2CZeroDBωR23
A metal disc of radius R rotates with an angular velcoity ω about an axis perpendicular to its plane passing through its centre in a magnetic field B acting perpendicular to the plane of the disc. Calculate the induced emf between the rim and the axis of the disc.
View SolutionA conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionRadius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
View SolutionA circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
View SolutionA circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
View Solution

