Six particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
The correct Answer is:A, B
To solve the problem of six particles situated at the corners of a regular hexagon of side length a, moving at a constant speed v and maintaining a direction towards the particle at the next corner, we can follow these steps:
1. Understanding the Movement:
Each particle moves towards the next particle in a circular path, forming a spiral inward towards the center of the hexagon.
2. Analyzing the Geometry:
The angle between the direction of motion of any two adjacent particles is 60∘ because the internal angles of a regular hexagon are 120∘, and the direction of motion forms a 60∘ angle with the line connecting the two particles.
3. Calculating the Component of Velocity:
When one particle moves towards the next, we need to find the component of its velocity that is directed towards the next particle.
- The component of the velocity v in the direction towards the next particle is given by:
vtowards=vcos(60∘)=v⋅12=v2
4. Relative Velocity:
Since both particles are moving towards each other, the effective relative velocity at which they approach each other is:
vrelative=v+vtowards=v+v2=3v2
5. Distance to Travel:
The distance each particle has to travel to meet the other is the side length of the hexagon, which is a.
6. Calculating Time to Meet:
The time t taken for the particles to meet can be calculated using the formula:
t=DistanceRelative Velocity=a3v2=2a3v
Final Answer:
The time taken for the particles to meet each other is:
t=2a3v
Each particle moves towards the next particle in a circular path, forming a spiral inward towards the center of the hexagon.
The angle between the direction of motion of any two adjacent particles is 60∘ because the internal angles of a regular hexagon are 120∘, and the direction of motion forms a 60∘ angle with the line connecting the two particles.
When one particle moves towards the next, we need to find the component of its velocity that is directed towards the next particle.
- The component of the velocity v in the direction towards the next particle is given by:
vtowards=vcos(60∘)=v⋅12=v2
Since both particles are moving towards each other, the effective relative velocity at which they approach each other is:
vrelative=v+vtowards=v+v2=3v2
The distance each particle has to travel to meet the other is the side length of the hexagon, which is a.
The time t taken for the particles to meet can be calculated using the formula:
t=DistanceRelative Velocity=a3v2=2a3v
The time taken for the particles to meet each other is:
t=2a3v
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective 2
10 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
Similar Questions
six particles are situated at the corners of a regular hexagon. These particles start moving with equal speed of 10 m/s in such that velocity of any one particle is directed towards the next particle. Find the rate (in m/s) at which length of a side of the hexagon is decreasing.
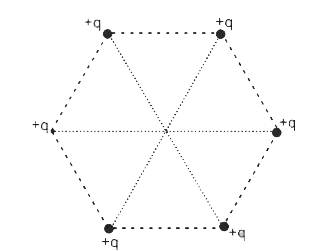
View SolutionSix equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
View Solution
Knowledge Check
Four particles situated at the corners of a square of side ‘a’ move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.
AavBa2vCa3vD2a3vThree particles of masses 1kg,2kg and 3kg are situated at the corners of an equilateral triangle move at speed 6ms−1,3ms−1 and 2ms−1 respectively. Each particle maintains a direction towards the particles at the next corners symmetrically. Find velocity of CM of the system at this instant
 A3ms−1B5ms−1C6ms−1Dzero
A3ms−1B5ms−1C6ms−1DzeroFour particles of masses 1 kg, 2 kg, 3 kg, and 4 kg are situated at the corners of a square and moving at speed 3ms−1,4ms−1,1ms−1 and 2ms−1 respectively. Each particle maintains a direction towards the particle at the next comer symmetrically. The momentum of the system at this instant is
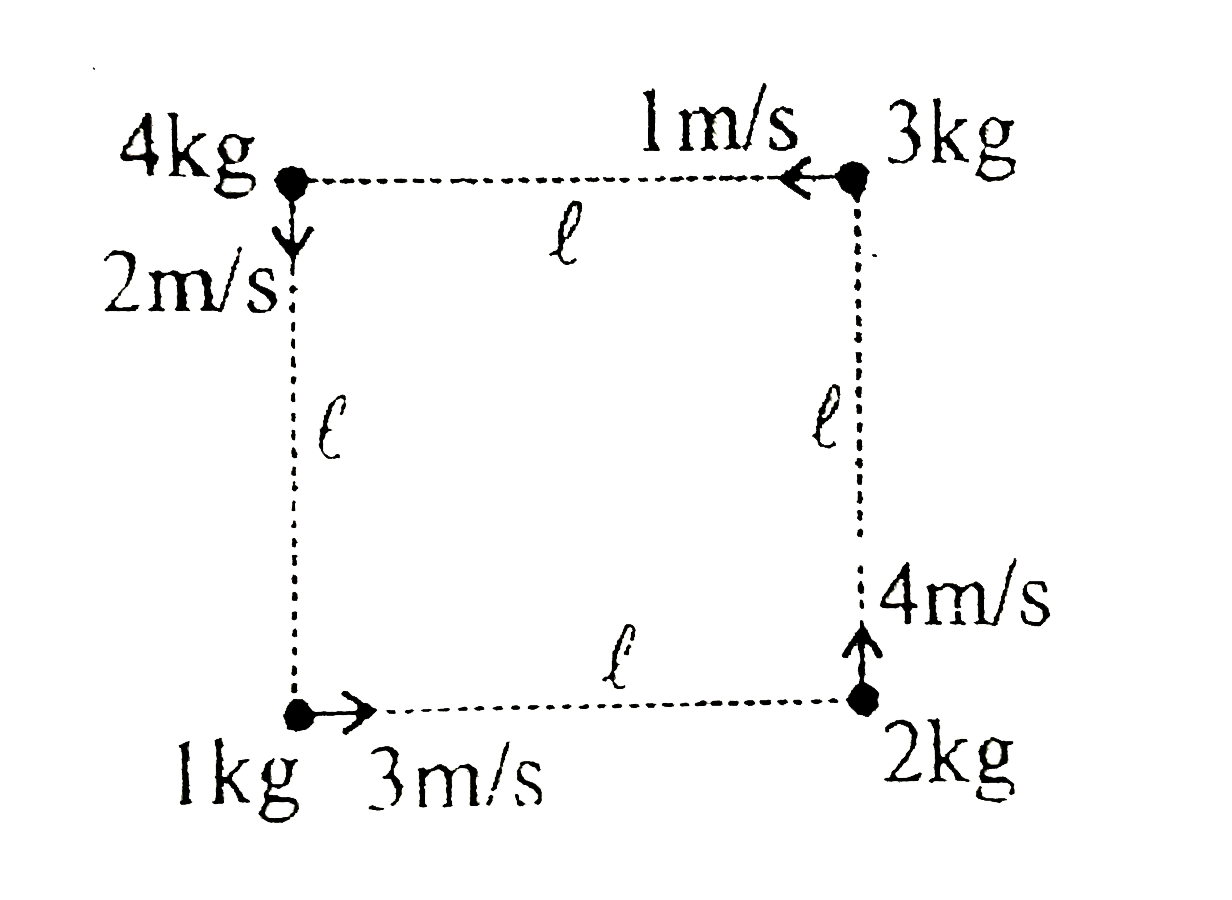 A3kgms−1B5kgms−1C6kgms−1DZero
A3kgms−1B5kgms−1C6kgms−1DZero
Four particles A,B,CandD are situated at the cornerst of a square ABCD of side aatt−0. Each of particles moves with constant speed (v). A always has its velocity along AB,B along BC,C along CB~andD along DA. At what time will these particles meet each other ?
View SolutionSix identical particles each of mass m are arranged at the corners of a regular hexagon of side length L. If the mass of one of the particle is doubled, the shift in the centre of mass is
View SolutionA particle is moving in a circle with a constant speed, the acceleration of the particle has
View SolutionSix particles each of massm are placed at the corners of a regular hexagon of edge length a. If a point mass m0 is placed at the centre of the hexagon, then the net gravitational force on the point mass is
View SolutionA particle moves along a semicircular path of radius R in time t with constant speed. For the particle calculate
View Solution
