Solve the foregoing problem for the case of two concentric spheres of

The figure shows a system of two concentric spheres of radii $r_{1} and r_{2}$ are kept at temperature $T_{1} and T_{2}$ , respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to

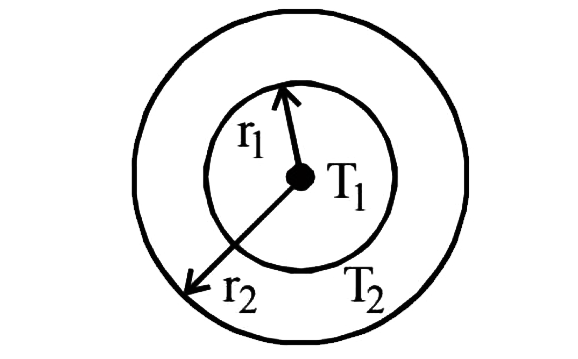A $I n (\frac{r_{2}}{r_{1}})$
B $\frac{r_{2} - r_{1}}{r_{1} r_{2}}$
C $(r_{1} - r_{2})$
D $\frac{r_{1} r_{2}}{r_{2} - r_{1}}$
The capacitance of two concentric spherical shells of radii $R_{1}$ and $R_{2} (R_{2} > R_{1})$ is
A $4 π ε_{0} R_{2}$
B $4 π ε_{0} \frac{(R_{2} - R_{1})}{R_{1} R_{2}}$
C $4 π ε_{0} \frac{R_{1} R_{2}}{(R_{2} - R_{1})}$
D $4 π ε_{0} R^{1}$
A system consists of two concentric spherical shells of radii $a$ and $b (b > a)$ maintained at temperature $T_{1}$ and $T_{2}$ respectively. The radial rate of flow of heat through substance between the two concentric spherical shells is proportional to
Ab - a
B $\frac{a b}{b - a}$
C ${log}_{e} (\frac{b}{a})$
D $\frac{b - a}{a b}$

Solve the foregoing problem for the case of two concentric spheres of radii $R_{1}$ and $R_{2}$ and temperatures $T_{1}$ and $T_{2}$ .