Solve the previous problem if the firction coefficient between the 2.0 kg block and the plane below it is 0.5 and the plane below the 4.0 kg block is frictionless.

Text Solution

Verified by Experts

The correct Answer is:A, B

$m_{1} = 4, m_{2} = 2 k g$
FricitoN/Al coefficient between 2 kg block
and surface =0.5
R=10 cm=0.1m $< b r >$ I=0.5kg-m^2 $< b r >$ -m_1gsintheta-T_1 $< b r > = m_{1} a$ …..1
$- T_{2} - (m_{2} g sin θ + μ m_{2} g cos θ)$
$= m_{2} a$ …2
$(T_{1} - T_{2}) = \frac{I_{a}}{r^{2}}$ ……3
Adding equation 1 and 2 we will get
$m_{1} g sin θ - (m_{2} g sin θ - μ m g cos θ) + (T_{2} - T_{1})$
$= m_{a} + m_{2} a$
$= 4 \times 9.8 \times \frac{91}{\sqrt{2}}) < b r >$ {2xx9.8xx(1/sqrt2)+0.5xx2xx9.8xx(1/sqrt2)} $< b r >$ =(4+2+05/0.01)a $< b r >$ rarr 37.80-(13.90+6.95)=56a $< b r >$ rarr 27.8-20.3=56a $< b r >$ rarr a=7/56=0.125m/s^2

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the arrangement shown in figure coefficient of friction between $5 k g$ block and incline plane is $μ = 0.5$ . Friction force acting on the $5 k g$ block is

A $20 N$
B $15 N$
C $10 N$
D $5 N$
Question 2 - Select One or More
$1 k g$ and $4 k g$ blocks lie on a rough horizontal surface. The coefficient of friction between $4 k g$ blocks and surface is $0.2$ while the coefficient of firction between $1 k g$ blocks and the surface is $0.6$ . All the pulley shown in the figure are massless and frictionless and all strings are massless and frictionless and all strings are massless.

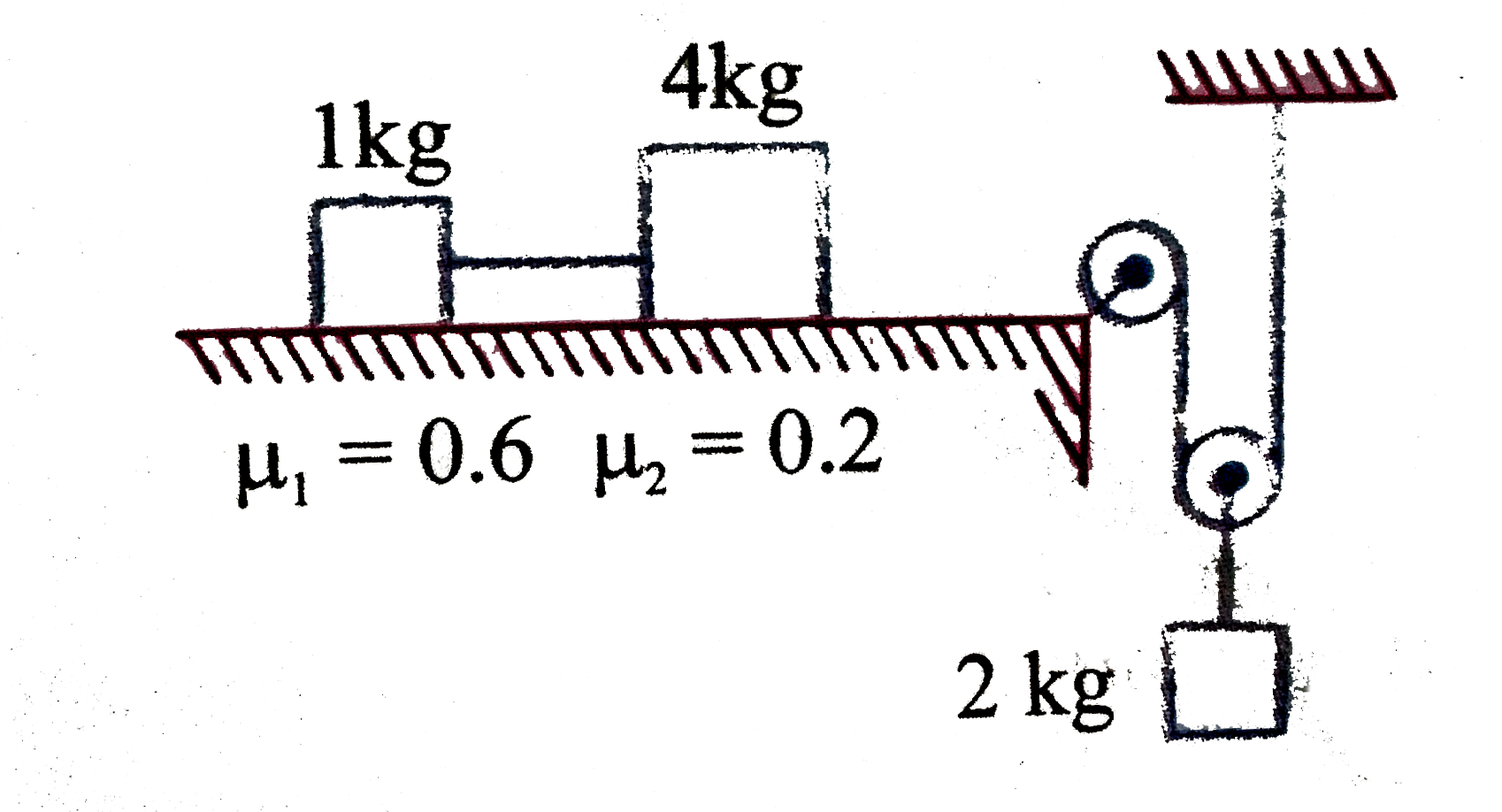AThe frictional force acting on $1 k g$ blocks is $2 N$ .
BThe frictional force acting on $1 k g$ block is $6 N$
CThe tension in the string connecting $4 k g$ block and $1 k g$ blocks is $1 N$
DThe tension in the string connecting $1 k g$ block and $4 k g$ blocks is zero.
Question 3 - Select One
A block rests on a rough inclined plane making an angle of $30^{\circ}$ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
A(a) 1.6
B(b) 4.0
C(c) 2.0
D(d) 2.5

HC VERMA ENGLISH-ROTATIONAL MECHANICS-Exercises

Home
Ask Doubt
Profile