Statement I: If a ball projected up obliquely from the ground breaks up into several fragments in its path, the centre of the system of all fragments moves in the same parabolic path compared to initial one till all fragments are in air.
Statement II: In the situation of Statement 1, at the instant of breaking, the fragments may be thrown in different directions with different speeds.
Both assertion and reason are true and reason is the correct explanation of assertion.
Both assertion and reason are true but reason is not the correct explanation of assertion.
Assertion is true and reason is false.
Assertion is false and reason is true.
The correct Answer is:B
To solve the problem, we need to analyze both statements provided and determine their validity based on the principles of the center of mass and projectile motion.
1. Understanding Statement I:
- The statement claims that if a ball projected obliquely breaks into several fragments during its flight, the center of mass of these fragments will continue to move in the same parabolic path as the original ball until all fragments are in the air.
- This is based on the principle of conservation of momentum. When the ball breaks, the total momentum of the system (the ball and its fragments) must be conserved. The center of mass continues to follow the same trajectory because external forces (like gravity) act uniformly on the system.
2. Analyzing Statement II:
- The second statement suggests that at the moment of breaking, the fragments can be thrown in different directions with different speeds.
- This is also true. When the ball breaks apart, the fragments can indeed have different velocities and directions due to the forces acting on them at that instant. However, this does not affect the trajectory of the center of mass.
3. Conclusion:
- Both statements are true. However, Statement II does not correctly explain Statement I. While the fragments may move in various directions, the center of mass still follows the original parabolic path due to the conservation of momentum.
- Therefore, the correct answer is that both statements are true, but Statement II is not a correct explanation of Statement I.
Final Answer:
- Statement I: True
- Statement II: True, but not a correct explanation of Statement I.
- The statement claims that if a ball projected obliquely breaks into several fragments during its flight, the center of mass of these fragments will continue to move in the same parabolic path as the original ball until all fragments are in the air.
- This is based on the principle of conservation of momentum. When the ball breaks, the total momentum of the system (the ball and its fragments) must be conserved. The center of mass continues to follow the same trajectory because external forces (like gravity) act uniformly on the system.
- The second statement suggests that at the moment of breaking, the fragments can be thrown in different directions with different speeds.
- This is also true. When the ball breaks apart, the fragments can indeed have different velocities and directions due to the forces acting on them at that instant. However, this does not affect the trajectory of the center of mass.
- Both statements are true. However, Statement II does not correctly explain Statement I. While the fragments may move in various directions, the center of mass still follows the original parabolic path due to the conservation of momentum.
- Therefore, the correct answer is that both statements are true, but Statement II is not a correct explanation of Statement I.
- Statement I: True
- Statement II: True, but not a correct explanation of Statement I.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Linked Comprehension105videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct141videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Statement I: In a two-body collision, the momenta of the particles are equal and opposite to one another, before as well as after the collision when measured in the centre of mass frame.
Statement. II: The momentum of the system is zero from the centre of mass frame.01:39View SolutionThree spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.
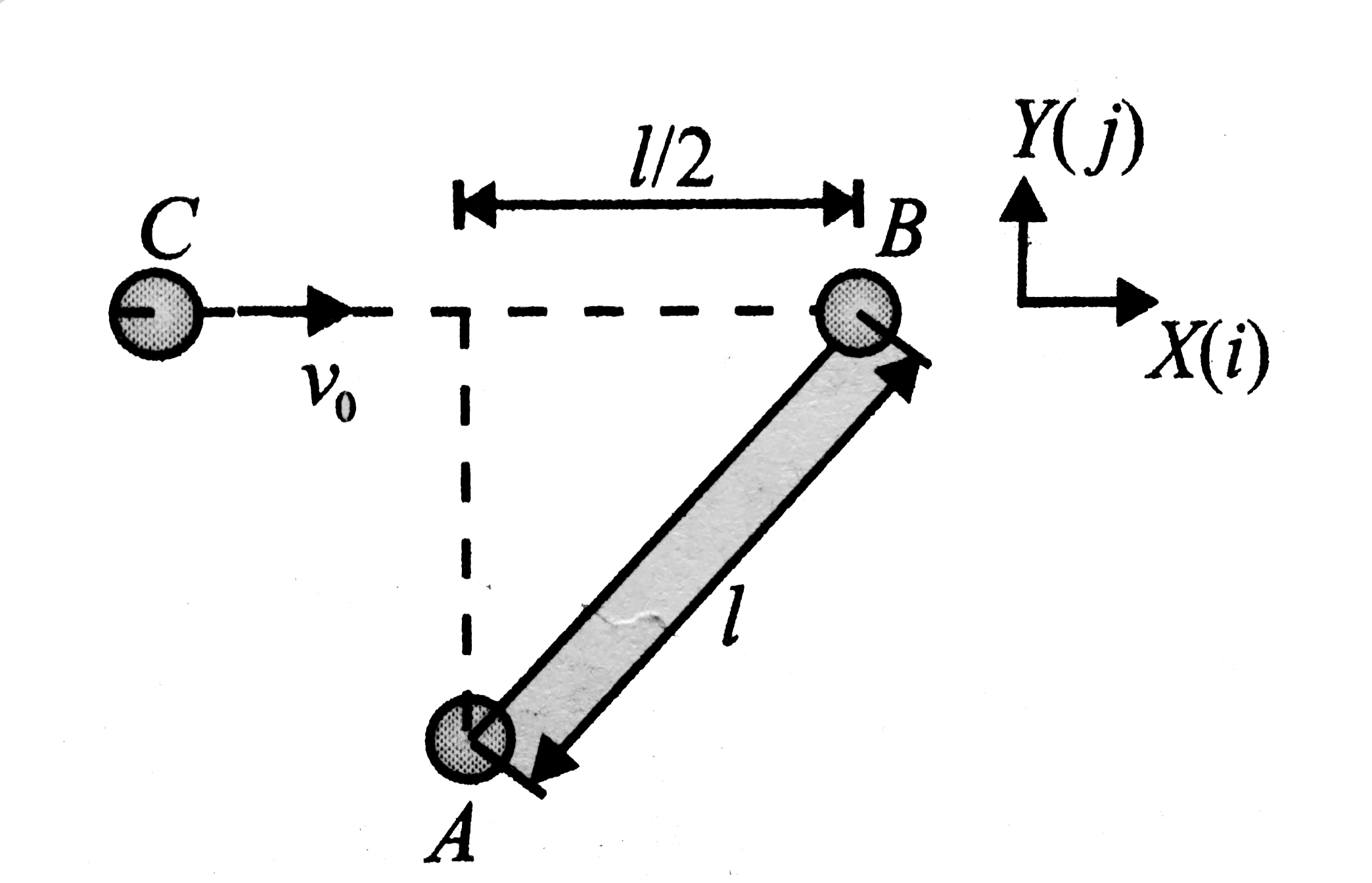
The magnitude of velocity of A immediately after collision is02:22View SolutionAn object initially at rest explodes into three equal fragments A,B and C.The momentum of A is pˆi and that of B is √3pˆj
where p is a+ve number. The momentum of C will be01:32View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.5View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View SolutionStatement I: If a ball projected up obliquely from the ground breaks up into several fragments in its path, the centre of the system of all fragments moves in the same parabolic path compared to initial one till all fragments are in air.
Statement II: In the situation of Statement 1, at the instant of breaking, the fragments may be thrown in different directions with different speeds.05:01View SolutionA fire cracker following a parabolic path explodes in mid air. The centre of mass of all the fragments will follow a path
03:41View SolutionBody breaks up into several fragments and each fragment starts to live as a new individual . This is __________ type of reproduction.
View SolutionBody breaks up into several fragments and each fragment starts to live as a new individual. This is asexual ( fragmentation) type of reproduction.
03:06View SolutionBody breaks up into several fragments and each fragment starts to live as a new individual. This is asexual ( fragmentation) type of reproduction.
View SolutionAn object is project with a speed 10ms^(-1) at an angle of 30^@ with the horizontal. It breaks into n equal fragments during its motion . One fragment strikes the ground at a distance of sqrt(3)m from the point of projection. The centre of mass of the remaining fragments strikes the ground at a distance of 7sqrt(3)m from the point of projection . If all fragments strike the ground at the same time , Find the value of n.
03:06View SolutionA body of mass m is projected at an angle g to the horizontal, the projectile at the highest point breaks into two fragments of equal masses. One of the fragments retraces its path to the point of projection. The velocity of the other fragment just after explosion is
View SolutionA body of mass m is projected at an angle theta to the horizontal, the projectile at the highest point breaks into two fragments of equal masses. One of the fragments retraces its path to the point of projection. The velocity of the other fragment just after explosion is
02:26View SolutionA bomb moving in a parabolic path explodes into two fragments of equal masses. The accelaration of the centre of mass of the fragments when both are in air is equal to
03:05View SolutionA body of mass m is projected at an angle θ to the horizontal, the projectile at the highest point breaks into two fragments of equal masses. One of the fragments retraces its path to the point of projection. The velocity of the other fragment just after explosion is
02:25View SolutionA bomb moving in a parabolic path explodes into two fragments of equal masses. The accelaration of the centre of mass of the fragments when both are in air is equal to
02:29View Solution

