Statement I: In free space a uniform spherical planet of mass M has a smooth narrow tunnel along its diameter. This planet and another superdense small particle of mass M start approaching towards each other from rest under action of their gravitational forces. When the particle passes through the centre of the planet, sum of kinetic energies of both the bodies is maximum.
Statement II: When the resultant of all forces acting on a particle or a particle like object (initially at rest) is constant in direction, the kinetic energy of the particle keeps on increasing.
Statement I is True, Statement II is True: Statement II is a correct explanation for Statement I.
Statement I is True, Statement II is True: Statement II is Not a correct explanation for Statement I.
Statement I is True, Statement II is False.
Statement I is False, Statement II is True.
The correct Answer is:A
Till particle reaches the centre of the planet, force on both the bodies are in direction on increasing. After the particle crosses the centre of the planet, forces on both are retarding in nature. Hence as the particle passes through the centre of the planet, sum of kinetic energies of oth the bodies is maximum. Therefore Statement 1 is true, Statement 2 is true: Statement 2 is a correct explanation for Statement 1.
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Linked Comprehension
23 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Integer
5 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionA planet revolves around the sun under the effect of its gravitational force. The torque acting on the planet due to the gravitational force is zero
View Solution
Knowledge Check
Two particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
Am1m2vBZeroC(m1−m2)vm1+m2Dm2m1vFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2)Two particles each of mass M and equidistant from each other move along a circle of radius R under the action of their mutual gravitional attraction the speed of each particle is
A√GM2RB12R√1GMC12√GMRD√4GMR
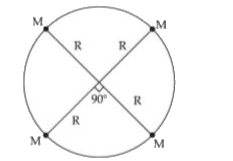
Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
View SolutionTwo particles of different masses initially at rest, start moving towards each other under their mutual gravitational attraction. At an instant when the speeds of the particles are v and 2v, the speed of the
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View Solution
A solid spherical planet of mass 2m and radius 'R' has a very small tunnel along its diameter. A small cosmic particle of mass m is at a distance 2R from the centre of the planet as shown. Both are initially at rest, and due to gravitational attraction, both start moving toward each other. After some time, the cosmic particle passes through the centre of the planet. (Assume the planet and the cosmic particle are isolated from other planets)
View SolutionA particle at a distance r from the centre of a uniform spherical planet of mass M radius R (ltr) has a velocity of magnitude v.
View Solution
