Statement I: The magnitude of the gravitational potential at the surface of solid sphere is less than that of the centre of sphere. Statement II: Due to the solid sphere, the gravitational potential is the same within the sphere.
Statement I is True, Statement II is True: Statement II is a correct explanation for Statement I.
Statement I is True, Statement II is True: Statement II is Not a correct explanation for Statement I.
Statement I is True, Statement II is False.
Statement I is False, Statement II is True.
The correct Answer is:C
To solve the question, we need to analyze both statements regarding the gravitational potential at the surface and the center of a solid sphere.
1. Understanding Gravitational Potential:
The gravitational potential V at a distance r from the center of a solid sphere of radius R and mass M is given by:
- For r≥R (outside the sphere):
V=−GMr
- For r<R (inside the sphere):
V=−GM2R+GMR3r2
Here, G is the gravitational constant.
2. Calculating Gravitational Potential at the Center:
At the center of the sphere (r=0):
Vcenter=−GM2R
3. Calculating Gravitational Potential at the Surface:
At the surface of the sphere (r=R):
Vsurface=−GMR
4. Comparing the Two Potentials:
We need to compare Vcenter and Vsurface:
- Vcenter=−GM2R
- Vsurface=−GMR
Since −GM2R is greater than −GMR (because a less negative value is greater), we conclude that:
|Vcenter|<|Vsurface|
Thus, the magnitude of gravitational potential at the surface is indeed greater than at the center.
5. Analyzing Statement II:
Statement II claims that the gravitational potential is the same within the sphere. However, from the formula for V inside the sphere, we see that it varies with r (the distance from the center). Therefore, this statement is false.
6. Conclusion:
- Statement I is true: The magnitude of the gravitational potential at the surface is greater than at the center.
- Statement II is false: The gravitational potential is not the same within the sphere.
Thus, the correct option is that Statement I is true, and Statement II is false.
Final Answer:
Option 3: Statement I is true, Statement II is false.
The gravitational potential V at a distance r from the center of a solid sphere of radius R and mass M is given by:
- For r≥R (outside the sphere):
V=−GMr
- For r<R (inside the sphere):
V=−GM2R+GMR3r2
Here, G is the gravitational constant.
At the center of the sphere (r=0):
Vcenter=−GM2R
At the surface of the sphere (r=R):
Vsurface=−GMR
We need to compare Vcenter and Vsurface:
- Vcenter=−GM2R
- Vsurface=−GMR
|Vcenter|<|Vsurface|
Thus, the magnitude of gravitational potential at the surface is indeed greater than at the center.
Statement II claims that the gravitational potential is the same within the sphere. However, from the formula for V inside the sphere, we see that it varies with r (the distance from the center). Therefore, this statement is false.
- Statement I is true: The magnitude of the gravitational potential at the surface is greater than at the center.
- Statement II is false: The gravitational potential is not the same within the sphere.
Option 3: Statement I is true, Statement II is false.
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Linked Comprehension
23 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Integer
5 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
The gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionDue to a solid sphere, magnitude of
View SolutionGravitational field due to a solid sphere
View SolutionThe gravitational potential at a point outside the solid sphere of radius "R" and at a distance of "r" will be :
View SolutionGravitational field at the surface of a solid sphere is 1.5×10−4N kg−1. Find the gravitational field at a point situated inside the sphere at a distance equal to half of rhe radius of the solid sphere.
View SolutionTwo spheres one of mass M has radius R. Another sphere has mass 4M and radius 2R. The centre to centre distance between them is 12R. Find the distance from the centre of smaller sphere where
(a) net gravitational field is zero,
(b) net gravitational potential is half the potential on the surface of larger sphere.
View SolutionAssertion: A positively charged rod is held near a neutral conducting solid sphere as illustrated below. The sphere lies on a insulated stand. The potential of ground (or earth) is zero. The potential at point A (point A need not be centre of the sphere) is higher compared to potential of gound (earth).
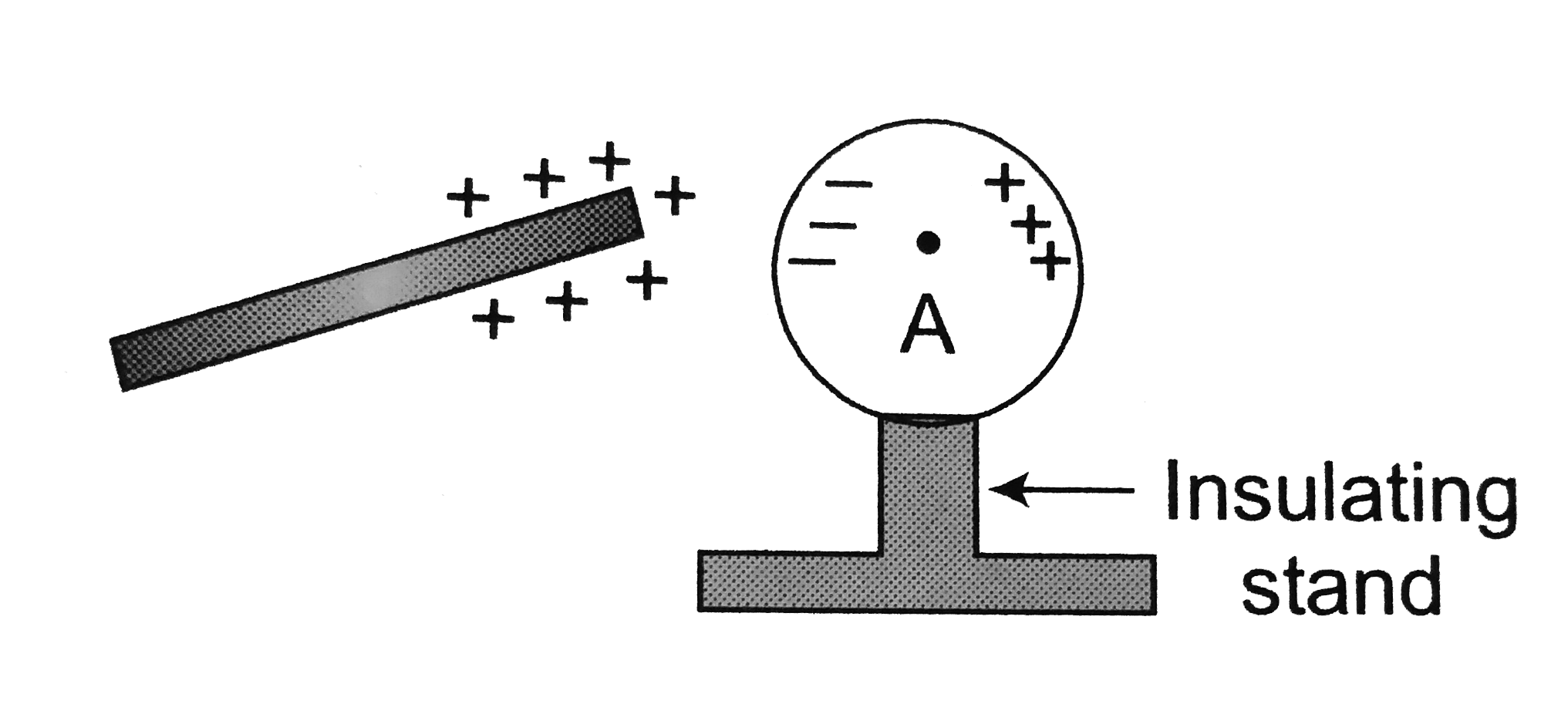
Reason: In this situation of assertion, the potential at the centre of conducting sphere is positive. the solid sphere being conducting, potential at each point in the sphere is same.
View SolutionAssertion: A positively charged rod is held near a neutral conducting solid sphere as illustrated below. The sphere lies on a insulated stand. The potential of ground (or earth) is zero. The potential at point A (point A need not be centre of the sphere) is higher compared to potential of gound (earth).

Reason: In this situation of assertion, the potential at the centre of conducting sphere is positive. the solid sphere being conducting, potential at each point in the sphere is same.
View SolutionTwo copper spheres of the same radii one hollow and the other solid are charged to same potential then
View SolutionTwo copper spheres of the same radii one hollow and the other solid are charged to same potential then
View Solution
