The arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a frictionless pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in (cm) of the spring. (g=10ms−2).
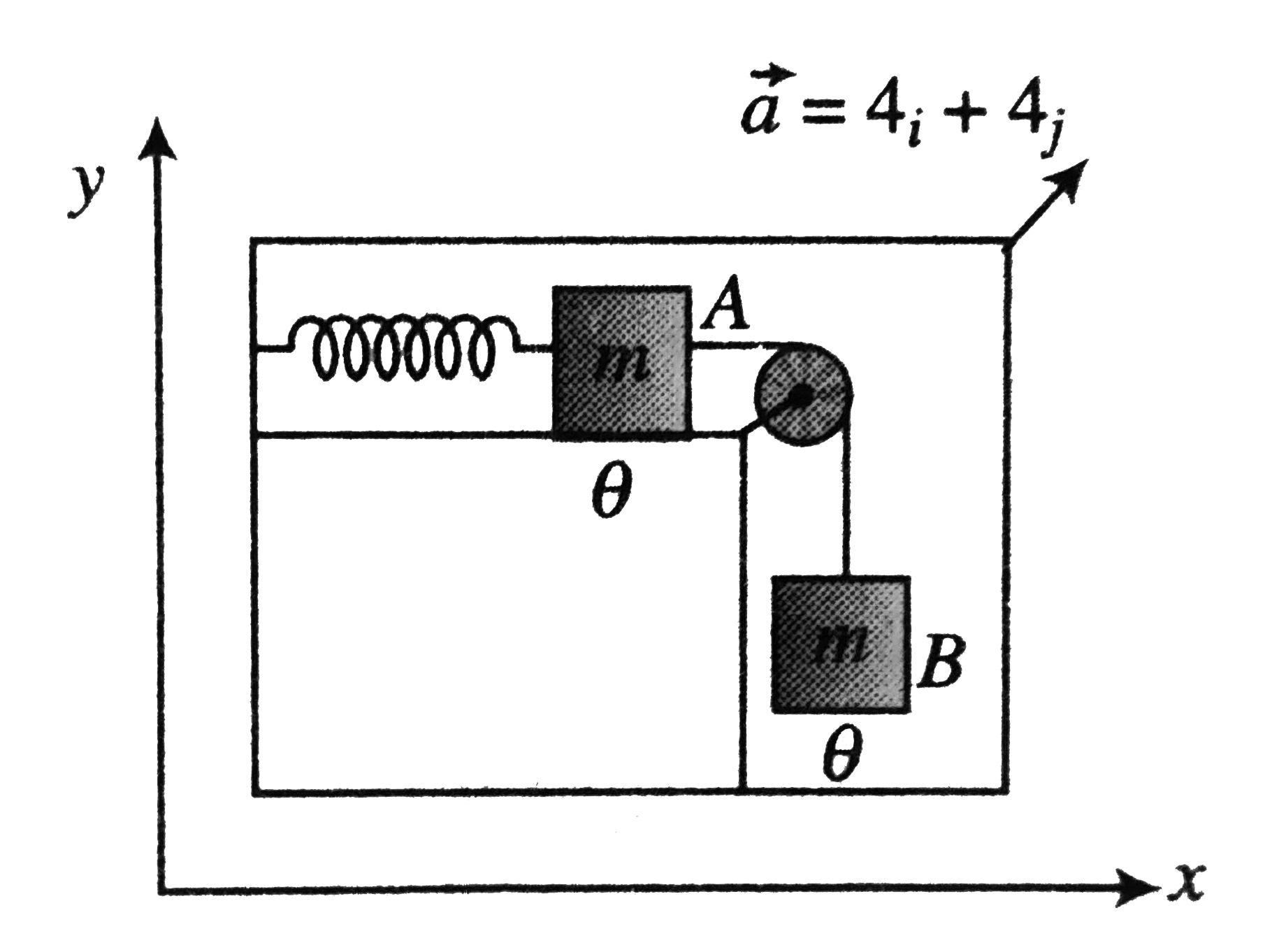
The correct Answer is:10
Let the maximum extension in spring be x.

Apply work-energy theorem: (Net work done by tension will be zero)
−12kx2−8x−7x+28x−2x=ΔKE=0
⇒−12×220x2+11x=0−x=0.1m=10cm
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )
19 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives(multiple Correct)
3 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a frictionless pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in (cm) of the spring. (g=10ms−2).

View SolutionThe arrangement shown in the diagram is moving in space with an acceleration a=4(ˆi+ˆj)m/s2. An ideal spring of natural length l0 having spring constant k=50N/m, is connected to block A. Blocks A and B are connected by an ideal string passing through a frictionless pulley. Mass of each block A and B is equal to m=2kg.
(a) Calculate the minimum value of coefficient of friction so that spring remains in its natural length. (b) If μ is reduced to (9/35)th of the original value, calculate the maximum extension of the spring.
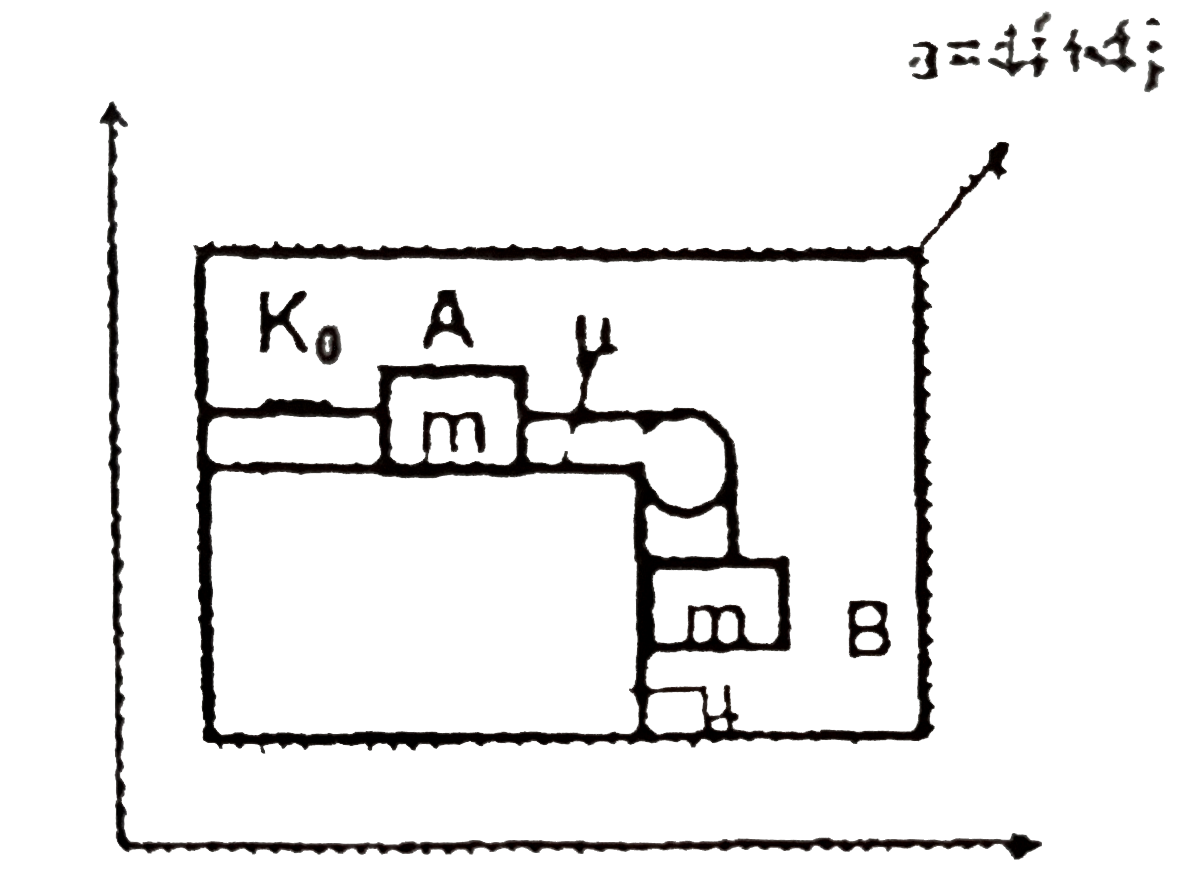
View Solution
Knowledge Check
Two blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
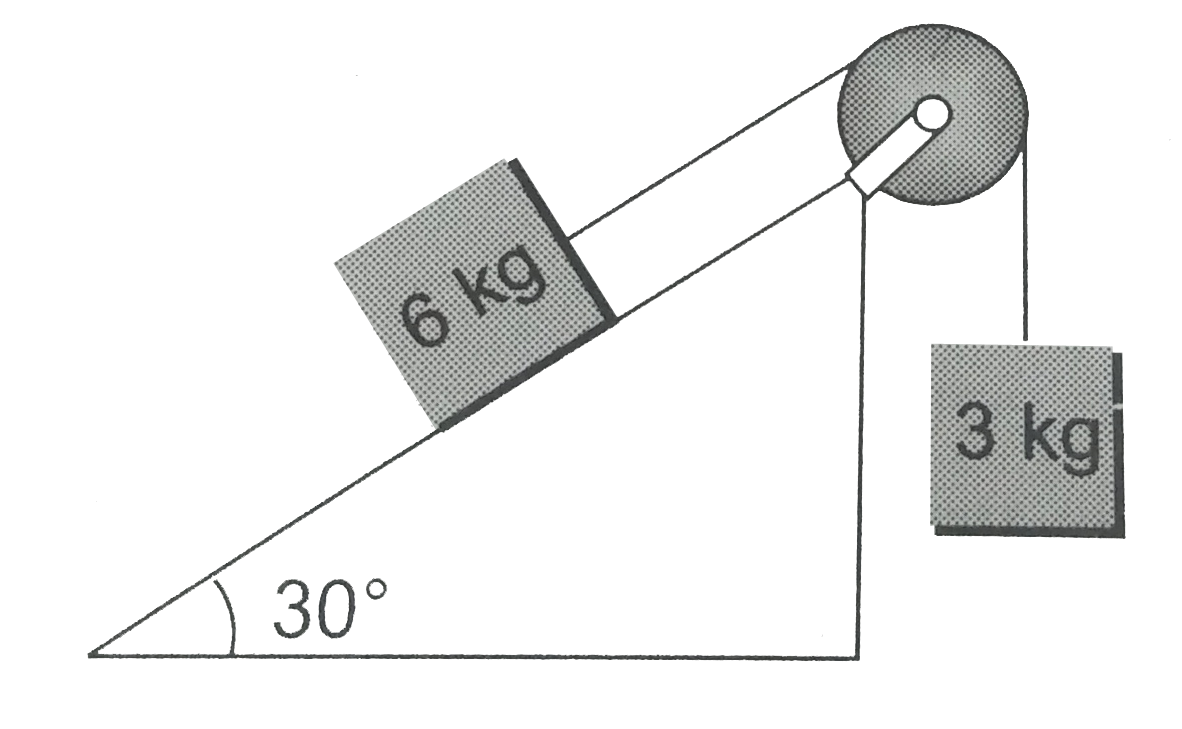 A4m/s2B2m/s2CzeroD6m/s2
A4m/s2B2m/s2CzeroD6m/s2Two blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
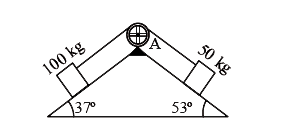
A50N up the planeB50N down the planeC100N up the planeD100N down the planeTwo blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
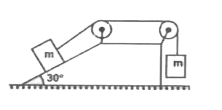 Ag/2Bg/4C2g/3D3g/4
Ag/2Bg/4C2g/3D3g/4
The two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
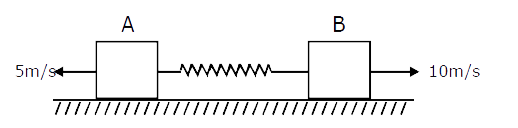
View SolutionTwo blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure. The acceleration of the blocks is :
View SolutionTwo blocks of masses m and 2m compress a spring of spring constant k by x0 and blocks are a connected by a thread and placed on a smooth surface as shown. Now , thread is burned. Find the speed of each block when the spring attains its normal length L.
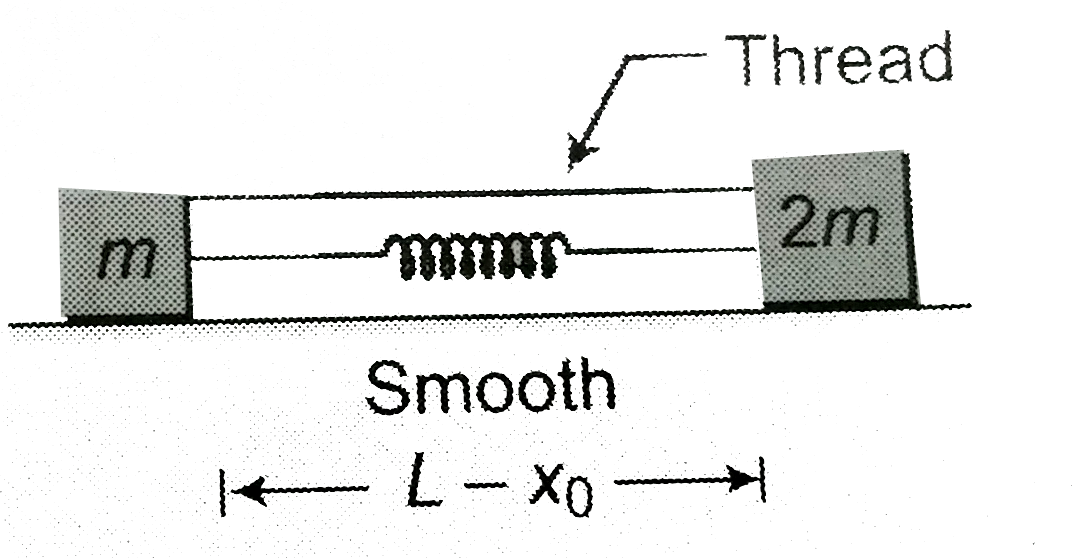
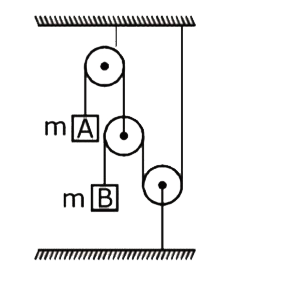
View SolutionIn the arrangement shown, the pulleys and the strings are ideal.The acceleration of the block B is
View SolutionTwo blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
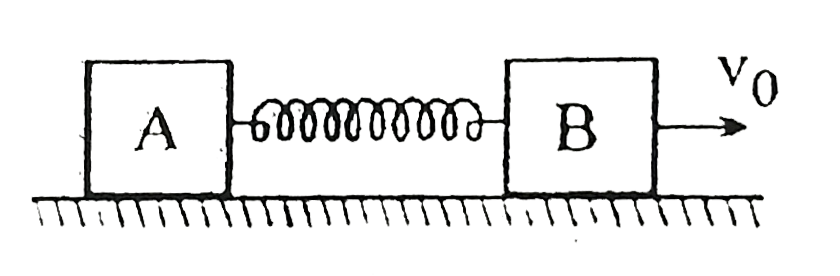
View Solution
