The ball is dropped from a bridge 122.5m above a rivet, After the ball has been falling for 2 s, a second ball is thrown straight down after it. What must its initial velocity be so that bothe hit the warer at the same time ?
To solve the problem step by step, we will analyze the motion of both balls and determine the initial velocity required for the second ball to hit the water at the same time as the first ball.
Step 1: Understand the motion of the first ball
The first ball is dropped from a height of 122.5 m. Since it is dropped, its initial velocity (u1) is 0 m/s. The time taken for the first ball to reach the water can be calculated using the equation of motion:
s=ut+12gt2
Where:
- s = distance fallen (122.5 m)
- u = initial velocity (0 m/s)
- g = acceleration due to gravity (approximately 9.8 m/s²)
- t = time taken to fall
Step 2: Calculate the time taken by the first ball
Substituting the known values into the equation:
122.5=0⋅t+12⋅9.8⋅t2
This simplifies to:
122.5=4.9t2
Now, solving for t2:
t2=122.54.9≈25
Taking the square root:
t≈5 seconds
Step 3: Determine the time for the second ball
The second ball is thrown 2 seconds after the first ball is dropped. Therefore, the time taken by the second ball to reach the water must be:
t2=t−2=5−2=3 seconds
Step 4: Set up the equation for the second ball
Let the initial velocity of the second ball be v. The distance it must cover is still 122.5 m. Using the same equation of motion for the second ball:
s=vt+12gt2
Substituting the known values:
122.5=v⋅3+12⋅9.8⋅(32)
This simplifies to:
122.5=3v+12⋅9.8⋅9
Calculating the second term:
12⋅9.8⋅9=44.1
So the equation becomes:
122.5=3v+44.1
Step 5: Solve for the initial velocity v
Rearranging the equation:
3v=122.5−44.1
Calculating the right side:
3v=78.4
Now, dividing by 3:
v=78.43≈26.13 m/s
Final Answer
The initial velocity v of the second ball must be approximately 26.1 m/s so that both balls hit the water at the same time.
---
The first ball is dropped from a height of 122.5 m. Since it is dropped, its initial velocity (u1) is 0 m/s. The time taken for the first ball to reach the water can be calculated using the equation of motion:
- s = distance fallen (122.5 m)
- u = initial velocity (0 m/s)
- g = acceleration due to gravity (approximately 9.8 m/s²)
- t = time taken to fall
Substituting the known values into the equation:
The second ball is thrown 2 seconds after the first ball is dropped. Therefore, the time taken by the second ball to reach the water must be:
Let the initial velocity of the second ball be v. The distance it must cover is still 122.5 m. Using the same equation of motion for the second ball:
Rearranging the equation:
The initial velocity v of the second ball must be approximately 26.1 m/s so that both balls hit the water at the same time.
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 Problems for practice
67 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 Problems for practice
45 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Problems for practice
25 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
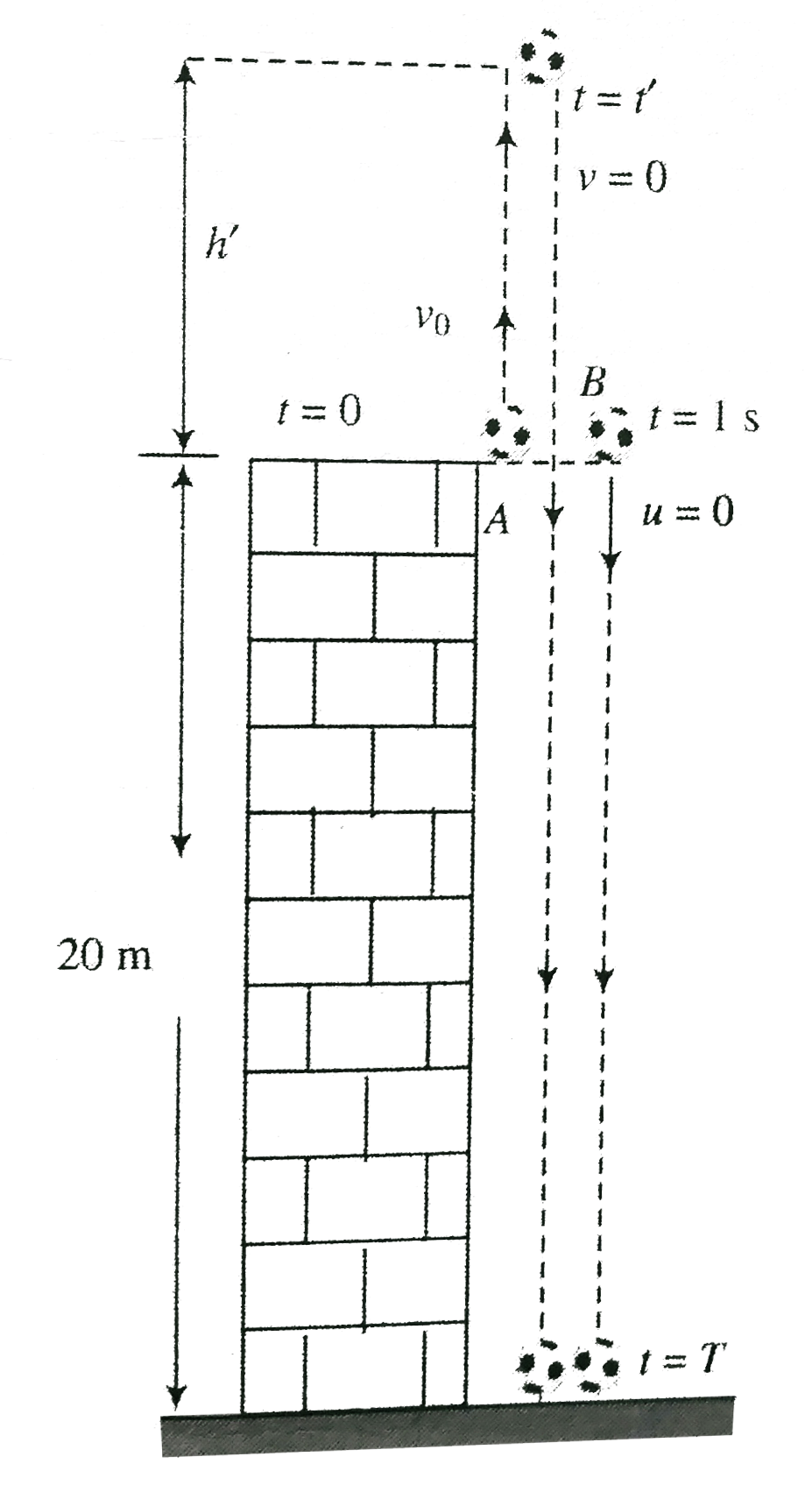
A ball is thrown straight up from the edge of the roof of a building .A second ball is dropped from the roof 1.00s later. You may ignore air resistance.
a. If the height of the buliding is 20.0m, what must the initial speed be of the first ball if both are to hit the ground at the same time? Consider the same situation, but now let the initial speed v0 of the first ball be given and treat the height (h) of the building as an unknown.
b. What must the height of the building be for both balls to reach the ground at the same time for each of the following values of v0: (i) 6.0ms−1 (ii) 9.5ms−1?
c. If v0 is greater than some values vmax, a value of (h) does same time. Solve for vmax. The value vmin also has a simple physical interpretation. What is it?
View SolutionA ball (A) is thrown straight upfrom the edge the roof of a building. Another ball (B) is dropped from the of 1.00s later. You may ignore air resistance . (a) If the height of the building id 20.0m, what must the initial speed of ball (A) he if bothe are to hit the ground at the same time? (b) On the function of time, measured fro when the first ball is thrown and take origin at ground.
 .
.
View Solution
Knowledge Check
A ball is dropped from a bridge at a height of 176.4 m over a river. After 2s, a second ball is thrown straight downwards. What should be the initial velocity of the second ball so that both hit the water simultaneously?
A2.45 m/sB49 m/sC14.5 m/sD24.5 m/sA ball is dropped from a bridge at a height of 176.4 m over a river .after 2 s a second ball is thrown straight downwards.what should be the initial velocity of the second ball so that both hit the water simultaneously ?
A2.45ms−1B49ms−1C14.5ms−1D24.5ms−1A ball is dropped from a bridge at a height of 176.4 m over a river .after 2 s a second ball is thrown straight downwards.what should be the initial velocity of the second ball so that both hit the water simultaneously ?
A2.45ms−1B49ms−1C14.5ms−1D24.5ms−1
A ball is thrown horizontally and at the same time another ball is dropped down from the top of a tower Will both the balls reach the ground at the same time ?
View SolutionA ball is dropped from a height 64 m above the ground and every time it hits the ground it rises to a height equal to half of the previous. What is the height attained after it hits the ground for the 16th time?
View SolutionA ball is dropped from a bridge at a height of 176.4 m over a river. After 2s a second ball is thrown straight downwards. What should be the initial velocity of the second ball so that both hit the water simultaneously ?
View SolutionA ball is drpped from rest at height 4h. After it has fallen a distance d, a second ball is dropped from rest at height h. What should d be (in terms of h) so that the balls hit the ground at the same time?
View SolutionA ball is dropped from a height of 20m on a floor for which e=1/2. The height attained by the ball after the second collision
View Solution
