The bob A of a simple pendulum is released when the string makes an angle of 45∘ with the vertical. It hits another bob B of the same material and same mass kept at rest on the table. If the collision is elastic, then

Both A and B rise to the same height.
Both A and B come to rest at B
Both A and B move with the same velocity of A
A comes to rest and B moves with the velocity of A
The correct Answer is:D
Due to the same mass of A and B as well as due to elastic collision, velocities of spheres get interchanged after the collision. So, A comes to rest and B moves with the velocity of A.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
The bob A of a simple pendulum released from 30∘ to the vertical hits another bobo B of the same mass at rest on a table as shown in figure. How high does the bob A rise after the collision ? Neglect the size of the bobs and assume the collision to be elastic.

View Solutionwhen the bob of a simple pendulum swings, the work done by tension in the string is :
View Solution
Knowledge Check
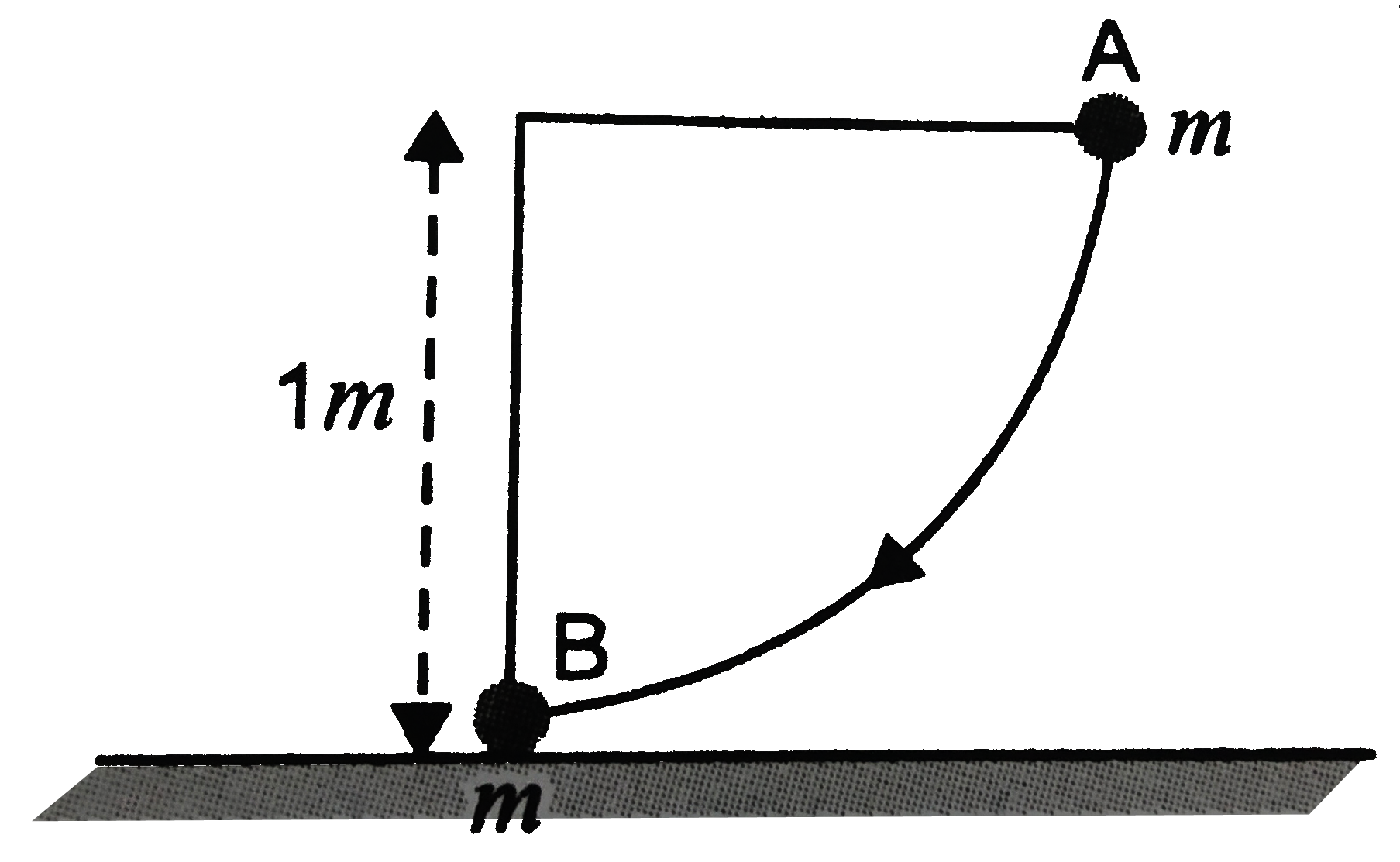
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
 A4.47ms−1B5.47ms−1C6.47ms−1D3.47ms−1
A4.47ms−1B5.47ms−1C6.47ms−1D3.47ms−1
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.

View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionA bob is attached to one end of a string other end of which is fixed at ped A. The bob is taken to a position where string makes an angle of 30∘ with the horizontal. On the circular path of the bob in vertical plane there is a peg'B' at a symmetrical position with respect to the position of release as shown in the figure. If Vc and Va be the minimum speeds in clockwise and anticlokwise direction respectively, given to the bob in order to hit the peg 'B' then ratio Vc:Va is equal to :

View SolutionA bob is attached to one end of a string other end of which is fixed at ped A. The bob is taken to a position where string makes an angle of 30∘ with the horizontal. On the circular path of the bob in vertical plane there is a peg'B' at a symmetrical position with respect to the position of release as shown in the figure. If Vc and Va be the minimum speeds in clockwise and anticlokwise direction respectively, given to the bob in order to hit the peg 'B' then ratio Vc:Va is equal to :

View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
View SolutionA simple pendulum of length l is pulled aside to make an angle θ with the vertical. Find the magnitude of the torque of the weight w of the bob about the point of suspension. When is the torque zero?
View Solution
