The bob of a pendulum is released from a horizontal position. If the lenght of the pendulum is 1.5 m what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?
Decrease in RE. of the bob in falling through a height l = Increase in its K.E.
mgl=12mv2
mv2=2mgl………..(1)
v=√2gl
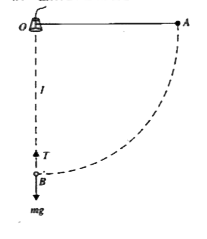
At the lowest position B, the forces acting on the bob are the tension in the string 7/acting vertically upward and the weight of the bob acting vertically downward. The resultant force gives the centripetal force.
mv2l=(T−mg), because the radius of the circular path r=L
T=mg+mv2l. But from equation (i) mv2=mgl
T=mg+2mgll=3mg
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
Explore 11 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (LONG ANSWER QUESTIONS)
Explore 8 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
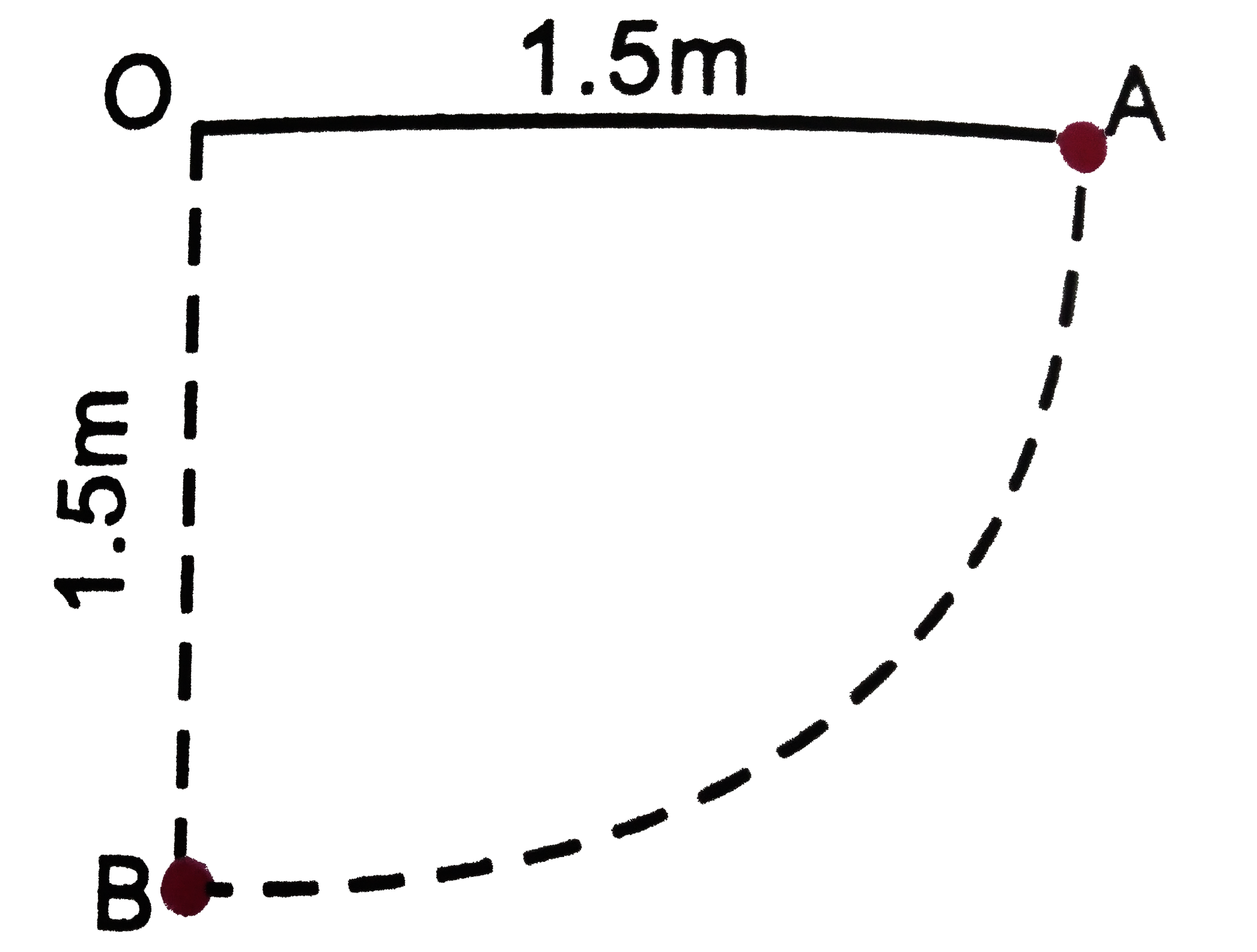
The bob A of a simple pendulum is released from a horizontal position A as shownin in figure. If the length of the pendulum is 1.5m , what is the speed with which the bob arrives at the lowermost point B, given that it dissipates 5% of its initial energy against air resistance ?
View SolutionA pendulum bob on a 2 m string is displaced 60∘ from the vertical and then released. What is the speed of the bob as it passes through the lowest point in its path
View Solution
Knowledge Check
The bob of a pendulum is released from a horizontal position. If the length of pendulum is 2 m, what is the speed with which the bob arrives at the lower most point. Assume that 10% of its energy is dissipated against air resistance.
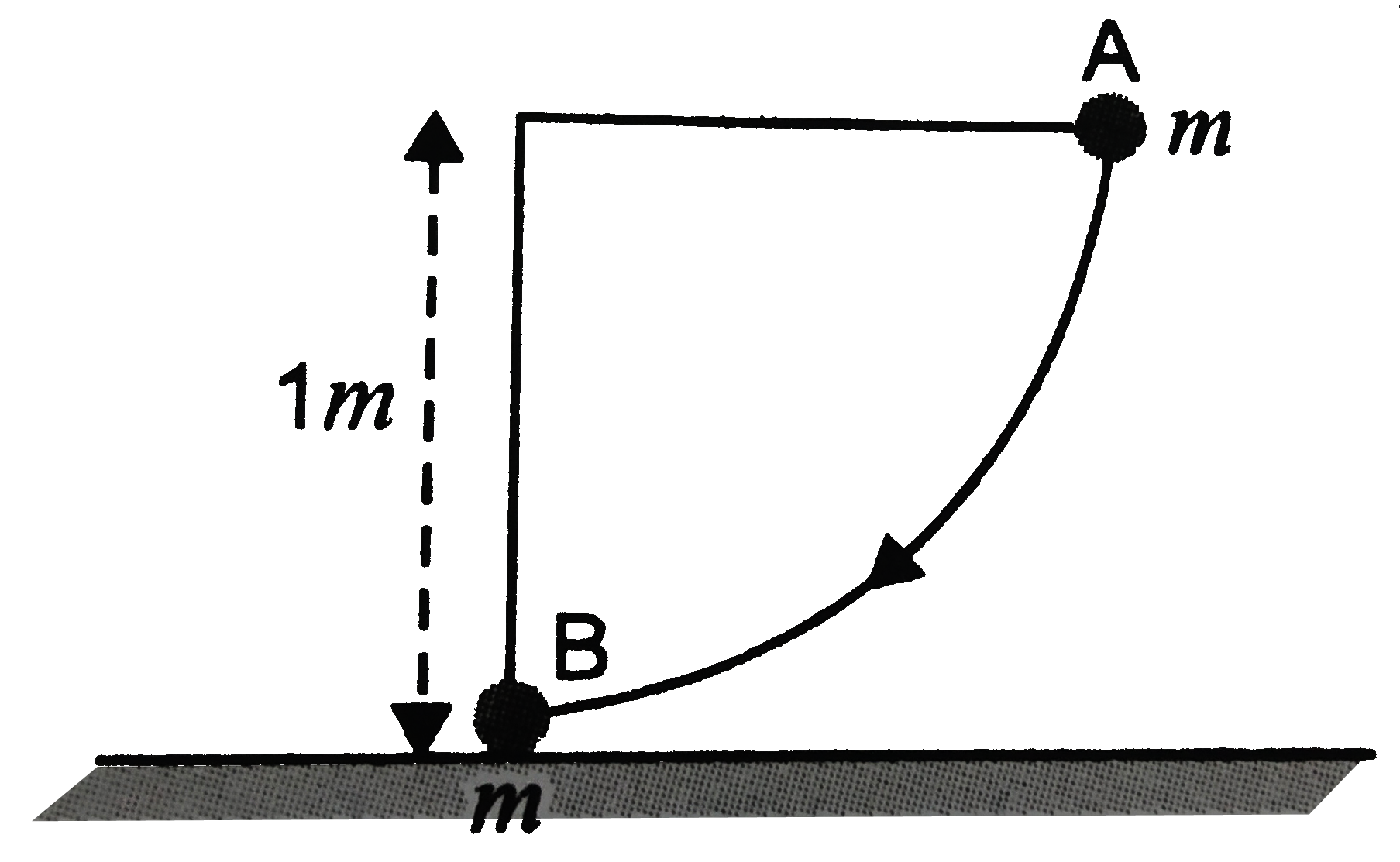
(Take g=10ms−2)A4ms−1B6ms−1C8ms−1D10ms−1The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
 A4.47ms−1B5.47ms−1C6.47ms−1D3.47ms−1
A4.47ms−1B5.47ms−1C6.47ms−1D3.47ms−1
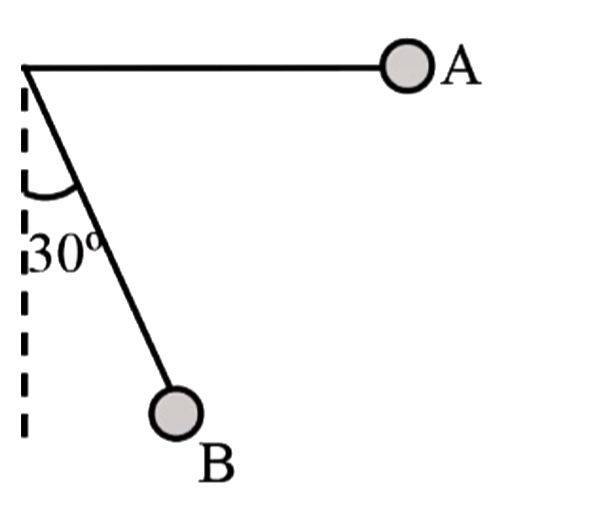
A simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
View SolutionThe bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with the upward vertical.
View SolutionThe bob of a simple pendulum of length l dropped from a horizontal position strikes a block of the same mass elastically, placed on a horizontal table (frictionless) as shown in the diagram, the block shall have kinetic energy-

View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.

View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View Solution