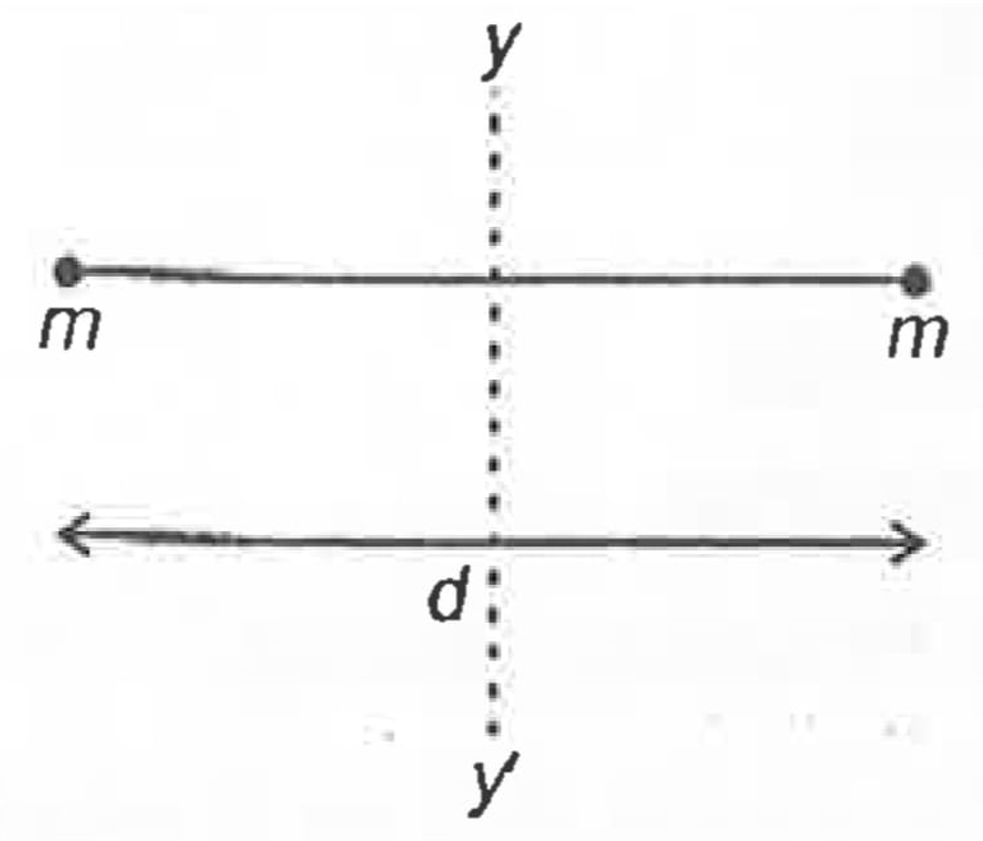
The centre of mass of two particles system lies
Step by step video & image solution for The centre of mass of two particles system lies by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE353videos
System of particles & rotational Motion
- BOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice90videos
ROTATIONAL MOTION
- BOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise449videos
Thermal Properties of Matter
Similar Questions
Knowledge Check
- Question 1 - Select One
Statement-1 : The centre of mass of a two particle system lies on the line joining the two particles, being closer to the heavier particle.
Statement-2 : Product of mass of one particle and its distance from centre of mass is numerically equal to product of mass of other particle and its distance from centre of mass.AStatement-1 is True, Statement-2 is True,
Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True,
Statement-2 is NOT a correct explanation for Statement-1CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is False - Question 2 - Select One
Find the distance between centre of gravity and centre of mass of a two particle system attached to the ends of a light rod. Each particle has same mass. Length of the rod is R, where R is the radius of earth.
_E01_014_Q01.png) ARBR/2CzeroDR/4
ARBR/2CzeroDR/4
Write an expression for the centre of mass of& two partide system
View SolutionThe centre of mass of three particles of masses 1kg,2kg and 3kg lies at the point (3m, 3m, 3m). Where should a fourth particle of mass 4 kg be positioned so that the centre of mass of the four particle system lies at the point (1m, 1m, 1m)?
View SolutionFind out the position of centre of mass of two particle system.
View SolutionObtain an expression for the position vector of centre of mass of a two particle system.
View Solution(i) A regular polygon has 2016 sides and r is the radius of the circle circumscribing the polygon. Particles of equal mass are placed at 2015 vertices of the polygon. Find the distance of the centre of mass of the particle system from the centre of the polygon.
(ii) In the last problem you have been asked to remove any one particle from the system so that the centre of mass of the remaining 2014 particles lies farthest from the geometrical centre of the polygon. Which particle will you remove ?View SolutionThe coordinates of the centre of mass of a system of three particles of mass 1g,2g and 3g are (2,2,2). Where should a fourth particle of mass 4 g be positioned so that the centre of mass of the four particle system is at the origin of the three-dimensional coordinate system ?
View Solution