The current in a conductor and the potential difference across its ends are measured by an ammeter and a voltmeter.The meters draw negligible current.The ammeter is accurate but the vlotmeter has a zero error(that is ,it does not read zero when no potential difference is applied).Calculate the zero error if the readings for two different conditions are 1.75A, 14.4Vand 2.75a, 22.4V.
To solve the problem of calculating the zero error of the voltmeter, we will follow these steps:
Step 1: Understand the relationship between current, voltage, and resistance
According to Ohm's Law, the relationship between current (I), voltage (V), and resistance (R) is given by:
V=I⋅R
In this case, we have two different conditions with different currents and voltages.
Step 2: Set up the equations for both conditions
Let V be the zero error of the voltmeter. For the first condition:
I1⋅R=V1−V
Where:
- I1=1.75A
- V1=14.4V
For the second condition:
I2⋅R=V2−V
Where:
- I2=2.75A
- V2=22.4V
Step 3: Write the equations explicitly
From the first condition:
1.75R=14.4−V (1)
From the second condition:
2.75R=22.4−V (2)
Step 4: Rearrange the equations to isolate R
From equation (1):
R=14.4−V1.75
From equation (2):
R=22.4−V2.75
Step 5: Set the two expressions for R equal to each other
Since both expressions equal R, we can set them equal:
14.4−V1.75=22.4−V2.75
Step 6: Cross-multiply to eliminate the fractions
Cross-multiplying gives:
(14.4−V)⋅2.75=(22.4−V)⋅1.75
Step 7: Expand both sides
Expanding both sides results in:
39.6−2.75V=39.4−1.75V
Step 8: Rearrange to solve for V
Rearranging gives:
39.6−39.4=2.75V−1.75V
0.2=1V
Thus, we find:
V=0.2V
Step 9: Conclusion
The zero error of the voltmeter is 0.2V.
---
According to Ohm's Law, the relationship between current (I), voltage (V), and resistance (R) is given by:
V=I⋅R
In this case, we have two different conditions with different currents and voltages.
Let V be the zero error of the voltmeter. For the first condition:
I1⋅R=V1−V
Where:
- I1=1.75A
- V1=14.4V
I2⋅R=V2−V
Where:
- I2=2.75A
- V2=22.4V
From the first condition:
1.75R=14.4−V (1)
2.75R=22.4−V (2)
From equation (1):
R=14.4−V1.75
R=22.4−V2.75
Since both expressions equal R, we can set them equal:
14.4−V1.75=22.4−V2.75
Cross-multiplying gives:
(14.4−V)⋅2.75=(22.4−V)⋅1.75
Expanding both sides results in:
39.6−2.75V=39.4−1.75V
Rearranging gives:
39.6−39.4=2.75V−1.75V
0.2=1V
Thus, we find:
V=0.2V
The zero error of the voltmeter is 0.2V.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
The potential difference across a 4 H inductor vary with time is as shown. The current is Zero at t=0, Then the current at time t=2s
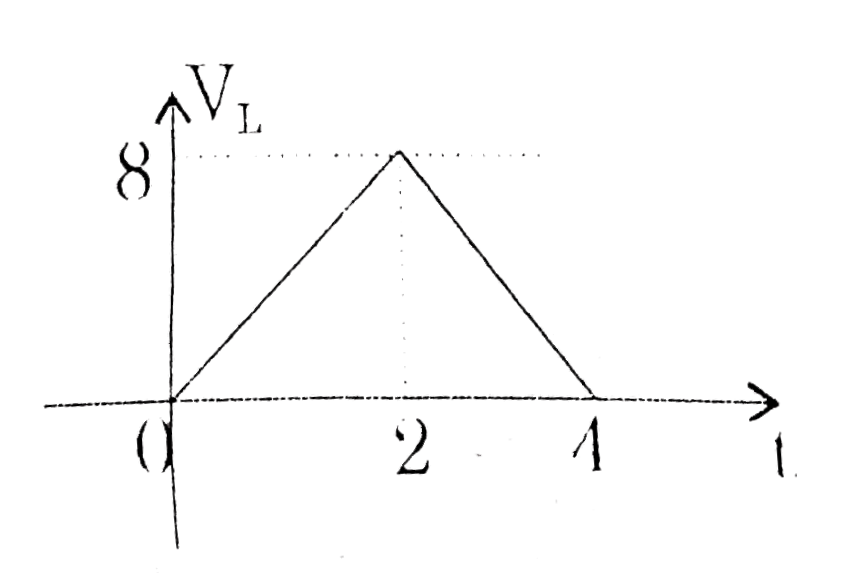
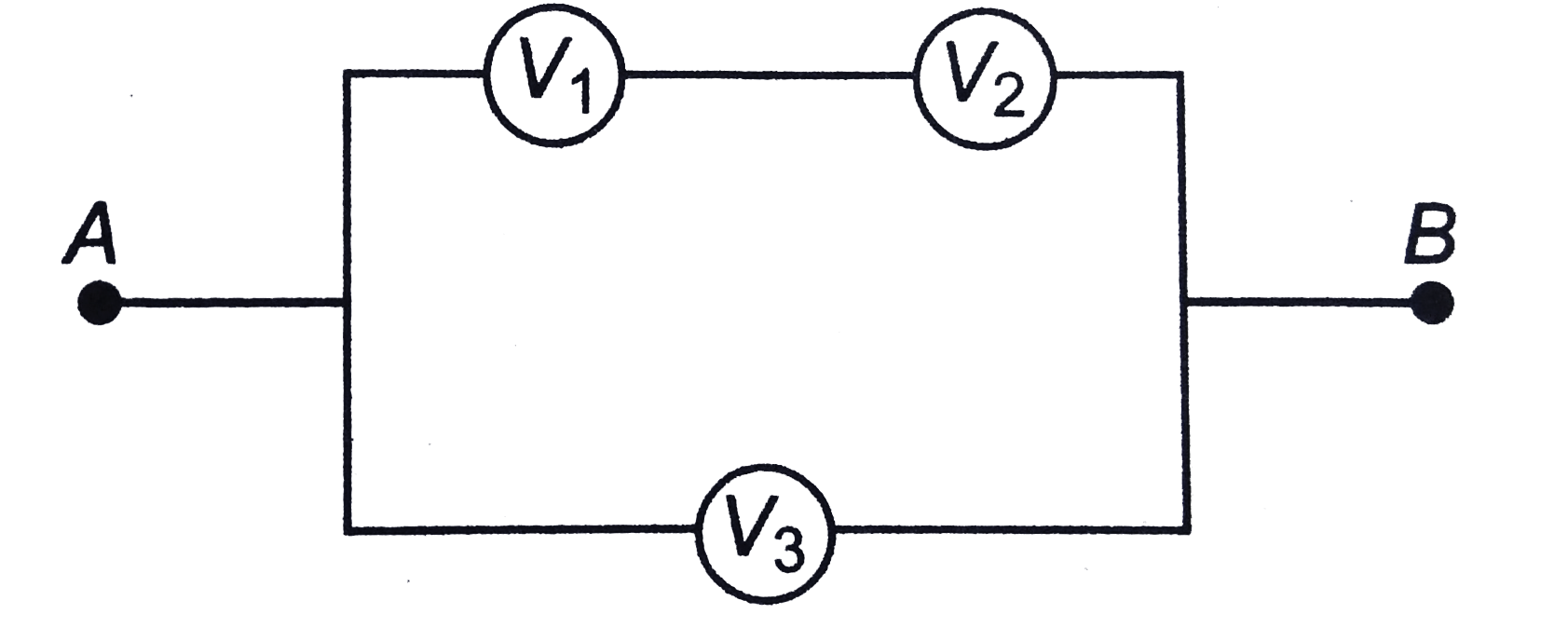
View SolutionThree voltmeters all having different resistance, are joined as shown. When some potential difference is applied acros A and B, their readings are V1,V2 and V3. Then
View SolutionCalculate the potential difference across the ends of a wire of resistance 2Ω'whenacurrentof1.5 A passes through it.
View SolutionThe potential difference across a 2-H inductor as a function of time is shown in Fig. At time t = 0, current is zero.
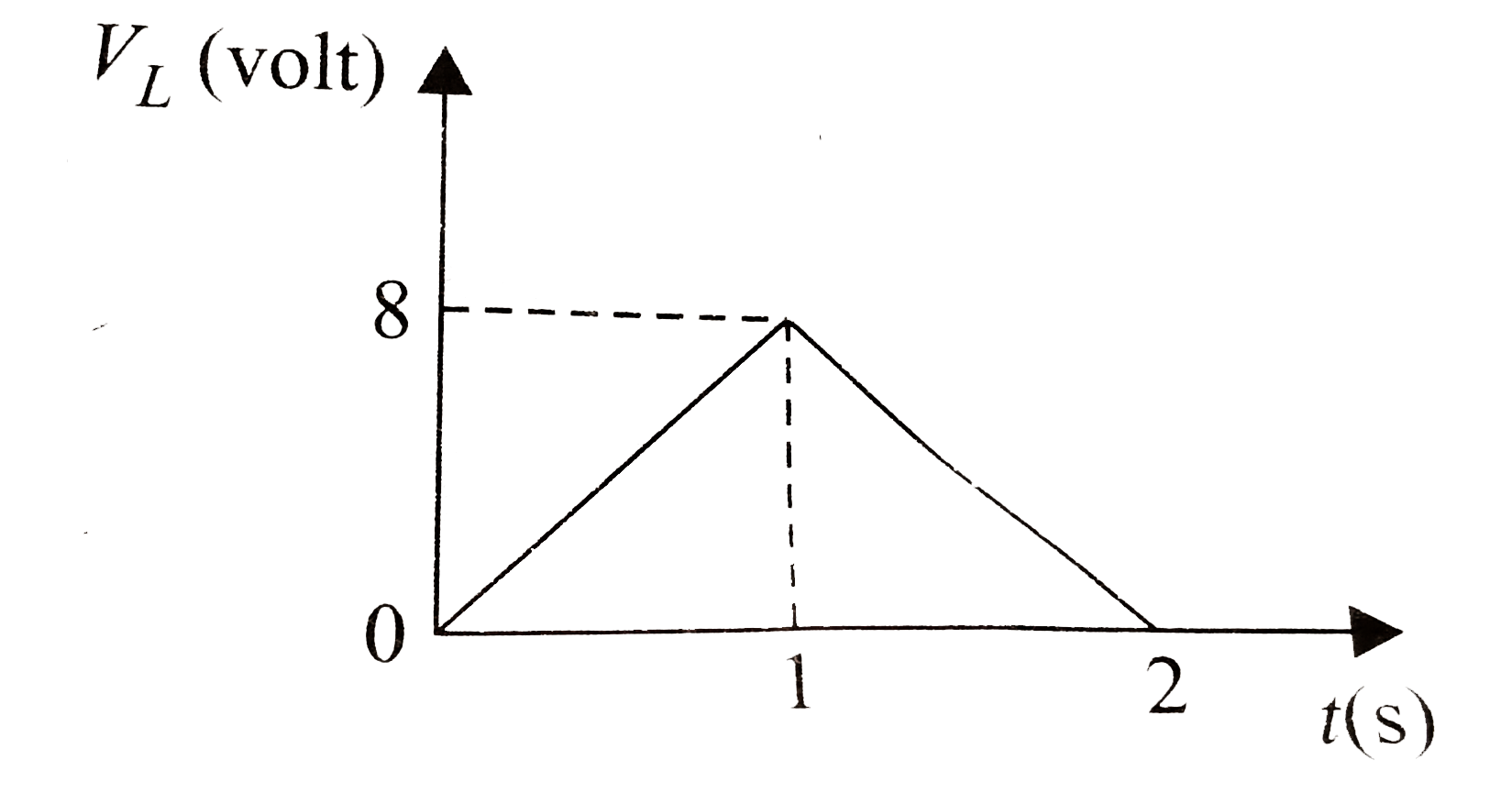
Current at t = 1 s is
View SolutionA resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the current in the circuit,
View SolutionThe potential difference across a 2-H inductor as a function of time is shown in Fig. At time t=0, current is zero.
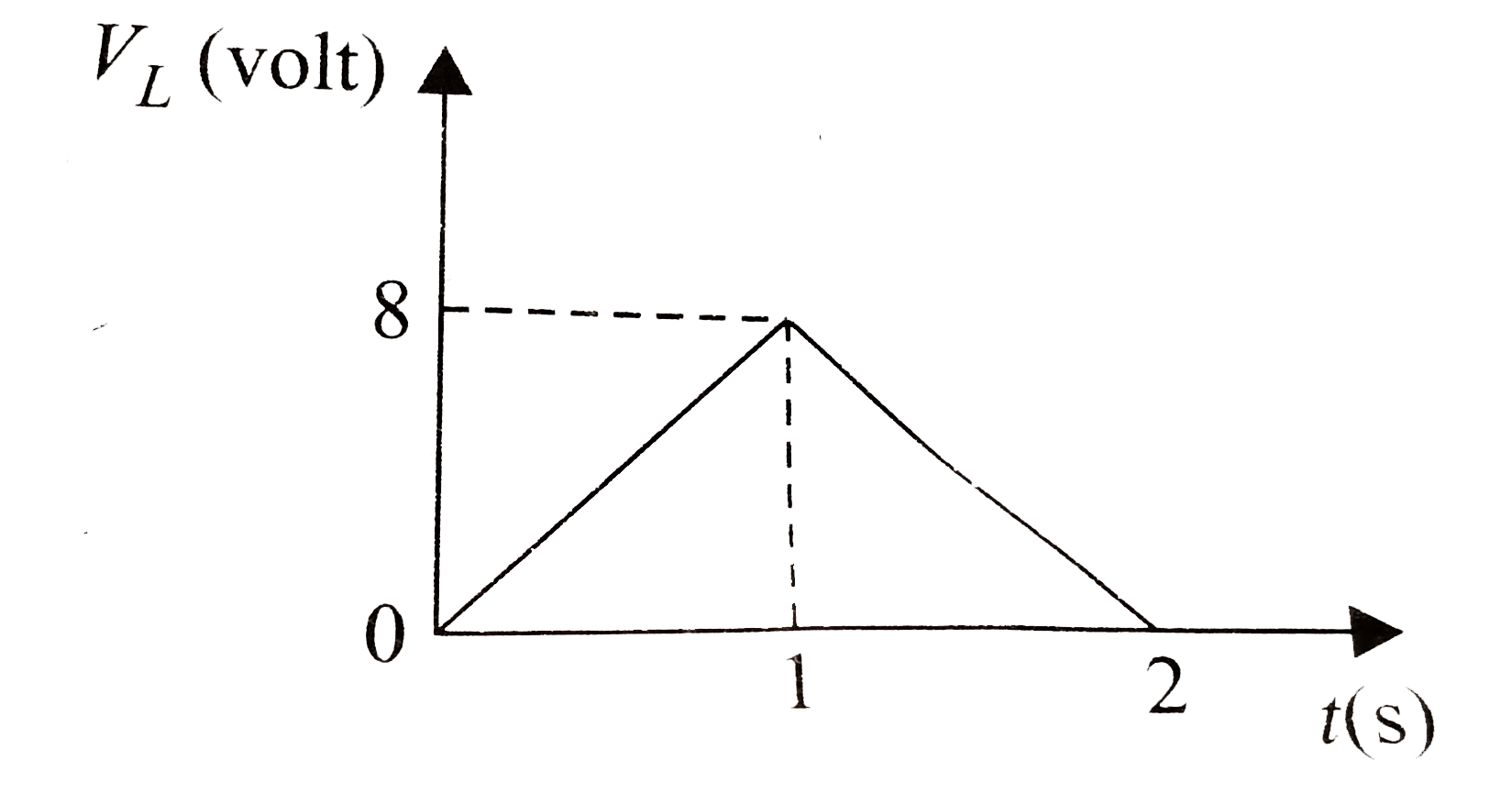
Area under VL−t graph gives
View SolutionAssertion : If potential difference across two points is zero, current between these two points should be zero.
Reason : Current passing from a resistor I=VR
View SolutionThe potential difference across a 150mH inductor as a function of time is shown in figure. Assume that the initial value of the current in the inductor is zero. What is the current when t=2.0ms? and t=4.0ms ?
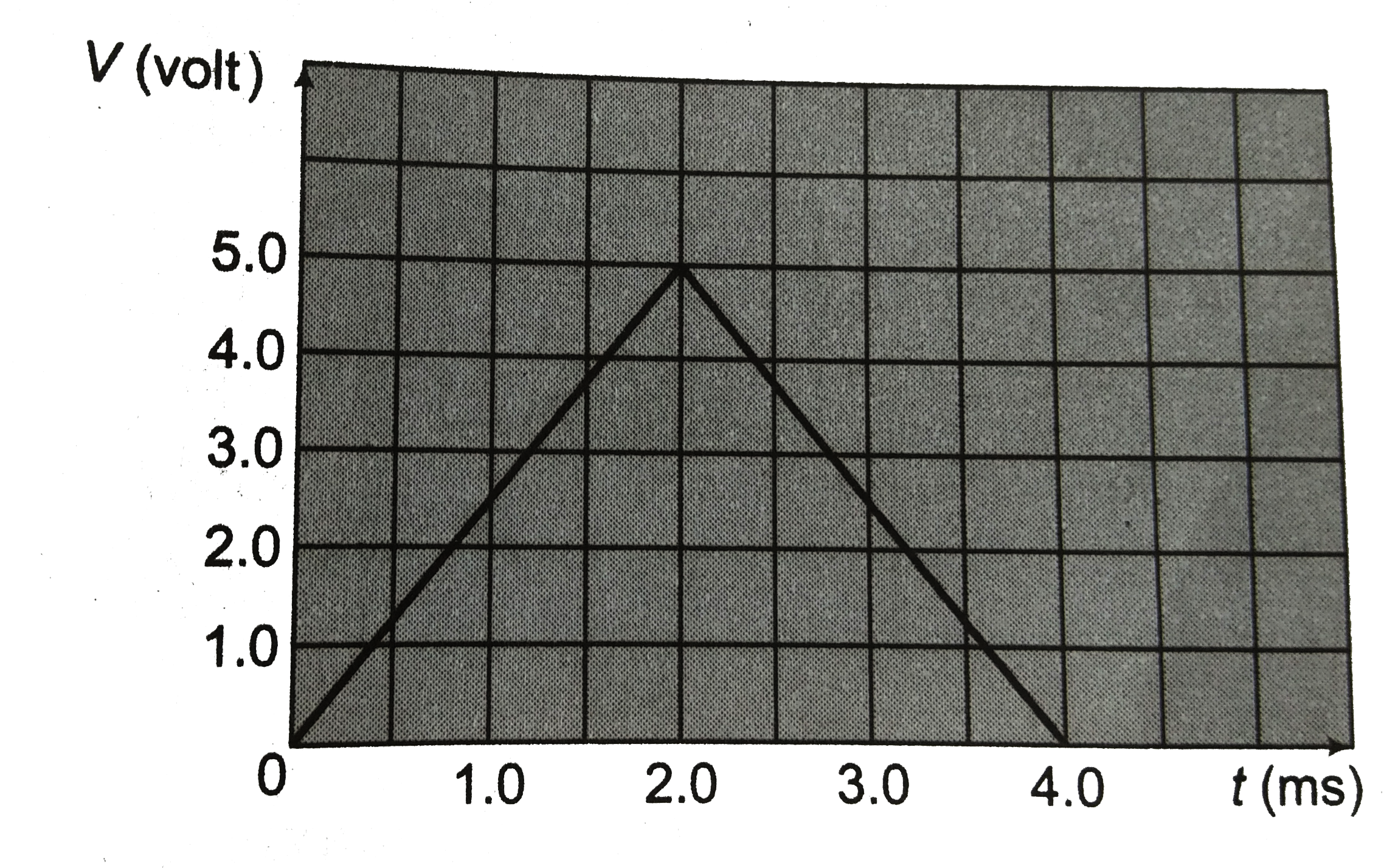
View SolutionWhen a potential difference of 2 volt is applied across the ends of a wire of 5 m length, a current of 1 A flows through it. Calculate :
the resistance across the ends of the wire if it is doubled on itself.
View SolutionThree resistances 2Ω,3Ω and 4Ω are connected in parallel. The ratio of currents passing through them when a potential difference is applied across its ends will be
View Solution
