A battery of emf 100V and a resistor of resistance 10k(Ω)are joined in series. This system is used as a source to supply current to an external resistance R. If R is not greater than 100(Ω), the current through it is constant up to two significant digits. Find its value, This is the basic principle of a constant-current source.
To solve the problem step-by-step, we will follow the principles of series circuits and Ohm's law.
Step 1: Identify the components and their values
- The electromotive force (emf) of the battery, V=100V
- The resistance of the internal resistor, R1=10kΩ=10,000Ω
- The external resistance, R, which is not greater than 100Ω.
Step 2: Calculate the total resistance in the circuit
Since the internal resistor and the external resistor are in series, the total resistance Rtotal can be calculated as:
Rtotal=R1+R
Given that R can be at most 100Ω:
Rtotal=10,000Ω+R
Since R can be at most 100Ω, the maximum value of Rtotal is:
Rtotal=10,000Ω+100Ω=10,100Ω
Step 3: Apply Ohm's Law to find the current
Ohm's Law states that:
I=VRtotal
Substituting the values we have:
I=100V10,100Ω
Step 4: Perform the calculation
Calculating the current:
I=10010,100≈0.00990099A
Step 5: Round to two significant digits
To express the current to two significant digits:
I≈0.0099A≈9.9mA
Final Answer
The current through the external resistance R is approximately 9.9mA.
---
- The electromotive force (emf) of the battery, V=100V
- The resistance of the internal resistor, R1=10kΩ=10,000Ω
- The external resistance, R, which is not greater than 100Ω.
Since the internal resistor and the external resistor are in series, the total resistance Rtotal can be calculated as:
Rtotal=R1+R
Given that R can be at most 100Ω:
Rtotal=10,000Ω+R
Since R can be at most 100Ω, the maximum value of Rtotal is:
Rtotal=10,000Ω+100Ω=10,100Ω
Ohm's Law states that:
I=VRtotal
Substituting the values we have:
I=100V10,100Ω
Calculating the current:
I=10010,100≈0.00990099A
To express the current to two significant digits:
I≈0.0099A≈9.9mA
The current through the external resistance R is approximately 9.9mA.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
Two resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionAn energy source will supply a constant current into the load if its internal resistance is
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 6 Ω resistor.
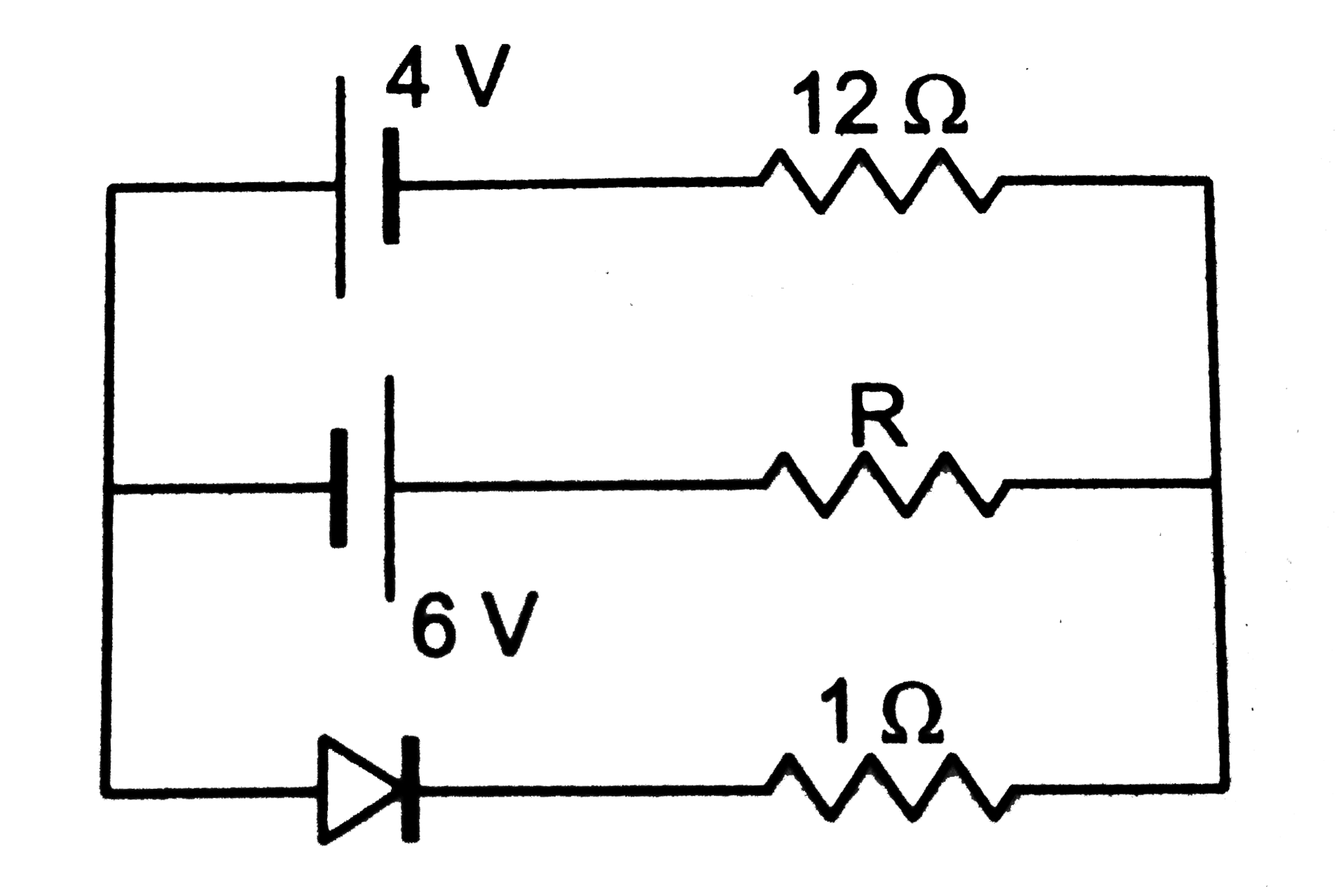
View SolutionFind the current through the resistance R in figure.If (a)R=12Ω(b)R=48Ω.
View Solution36 cells each of internal resistance 0.5Ω and emf 1.5 V each are used to send current through an external circuit of 2Ω resistance. Find the best mode of grouping them and the current through the external circuit.
View SolutionA car battery of emf 12V and internal resistance 0.05ω receives a current of 60 A from an external source, then the terminal potential difference of the battery is
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 3 Ω resistor,
View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of 10Ω through an ammeter of resistance 2Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistors ? What is the terminal voltage of the battery when the circuit is closed ?
View Solution
