A resistor of 6 is connected in series with another resistor of 4 . A potential difference of 20 V is applied across the combination. Calculate :
the current in the circuit,
To solve the problem step by step, we will follow these instructions:
Step 1: Identify the resistances in the circuit
We have two resistors connected in series:
- Resistor R1 = 6 Ω
- Resistor R2 = 4 Ω
Step 2: Calculate the equivalent resistance
In a series circuit, the total or equivalent resistance (R_eq) is the sum of the individual resistances:
Req=R1+R2
Substituting the values:
Req=6Ω+4Ω=10Ω
Step 3: Apply Ohm's Law
Ohm's Law states that the current (I) flowing through a conductor between two points is directly proportional to the voltage (V) across the two points and inversely proportional to the resistance (R):
V=I⋅R
We can rearrange this formula to find the current:
I=VReq
Step 4: Substitute the known values
We know the potential difference (V) is 20 V and the equivalent resistance (R_eq) is 10 Ω. Now we can substitute these values into the formula:
I=20V10Ω=2A
Step 5: Conclusion
The current in the circuit is:
I=2A
We have two resistors connected in series:
- Resistor R1 = 6 Ω
- Resistor R2 = 4 Ω
In a series circuit, the total or equivalent resistance (R_eq) is the sum of the individual resistances:
Req=R1+R2
Substituting the values:
Req=6Ω+4Ω=10Ω
Ohm's Law states that the current (I) flowing through a conductor between two points is directly proportional to the voltage (V) across the two points and inversely proportional to the resistance (R):
V=I⋅R
We can rearrange this formula to find the current:
I=VReq
We know the potential difference (V) is 20 V and the equivalent resistance (R_eq) is 10 Ω. Now we can substitute these values into the formula:
I=20V10Ω=2A
The current in the circuit is:
I=2A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C)
22 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C) MULTIPLE CHOICE TYPE)
2 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B) (MULTIPLE CHOICE TYPE)
3 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
Similar Questions
A resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the potential difference across the 6 Ω resistor.
View SolutionThree identical resistors are connected in series . When a certain potential difference is applied across the combination , the total power would be dissipated is 27W. How many times the power would be dissipated if the three resistors were connected in parallel across the same potential difference ?
View SolutionA cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the current in the circuit,
View SolutionA resistor circuit is constructed such that 12 resistor are arranged to form a cube as shown in fig. Each resistor has a resistance of 2Ω. The potential difference of 30V is applied across two of the opposing points as shown
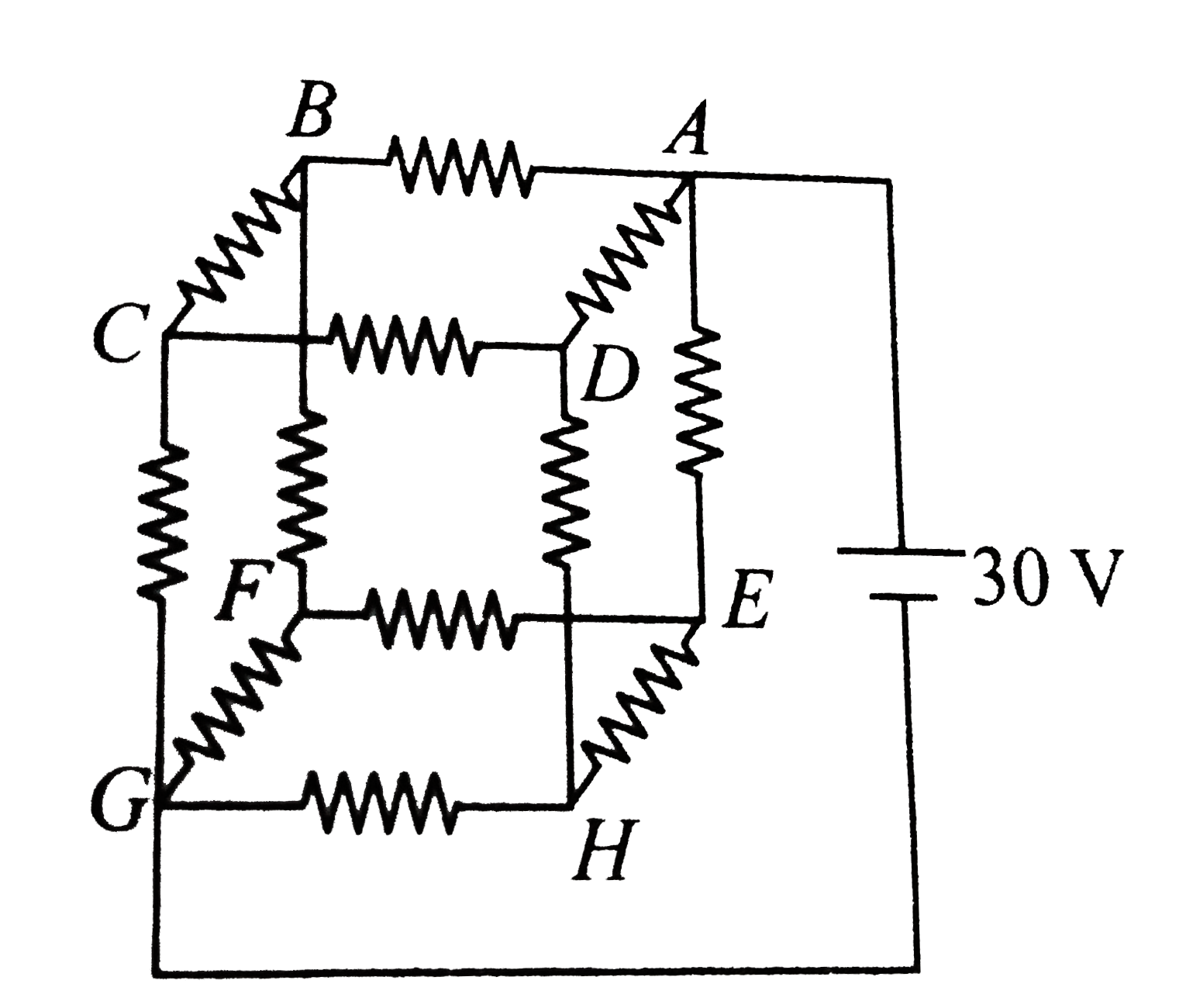
In question 20, the potential difference between the points C and G is
View SolutionAn inductor of inducance 5.0 H, having a negligible resistance, is connected in series with a 100Ω resistor and a battery of emf 2.0 V. Find the potential difference across the resistor 20 ms after the circuit is switched on.
View SolutionTwo resistors of 10KΩ and 20KΩ are conne cted in series. If tolerance of each resistor is 10% then tolerance of the combination will be
View SolutionIn the circuit diagram given below, a cell of 9 V and internal resistance of 0.5(Ω) is connected across a resistor A of 2Ω in series and two resistors of 2Ω and 6Ω in parallel.
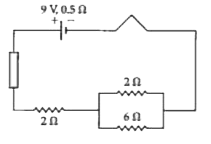
Find
The potential difference across the terminals of the cell.
View SolutionA 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the purpose of the resistor R?
View SolutionA cell supplies a current of 1.2 A through two resistors each of 2 Ω connected in parallel. When the resistors are connected in series, it supplies a current of 0.4 A. Calculate :
the internal resistance,
View Solution
