The density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the radio of ρ1ρ2

The correct Answer is:C
Let m1 be the mass of the core and m2 the mass of outer shell.
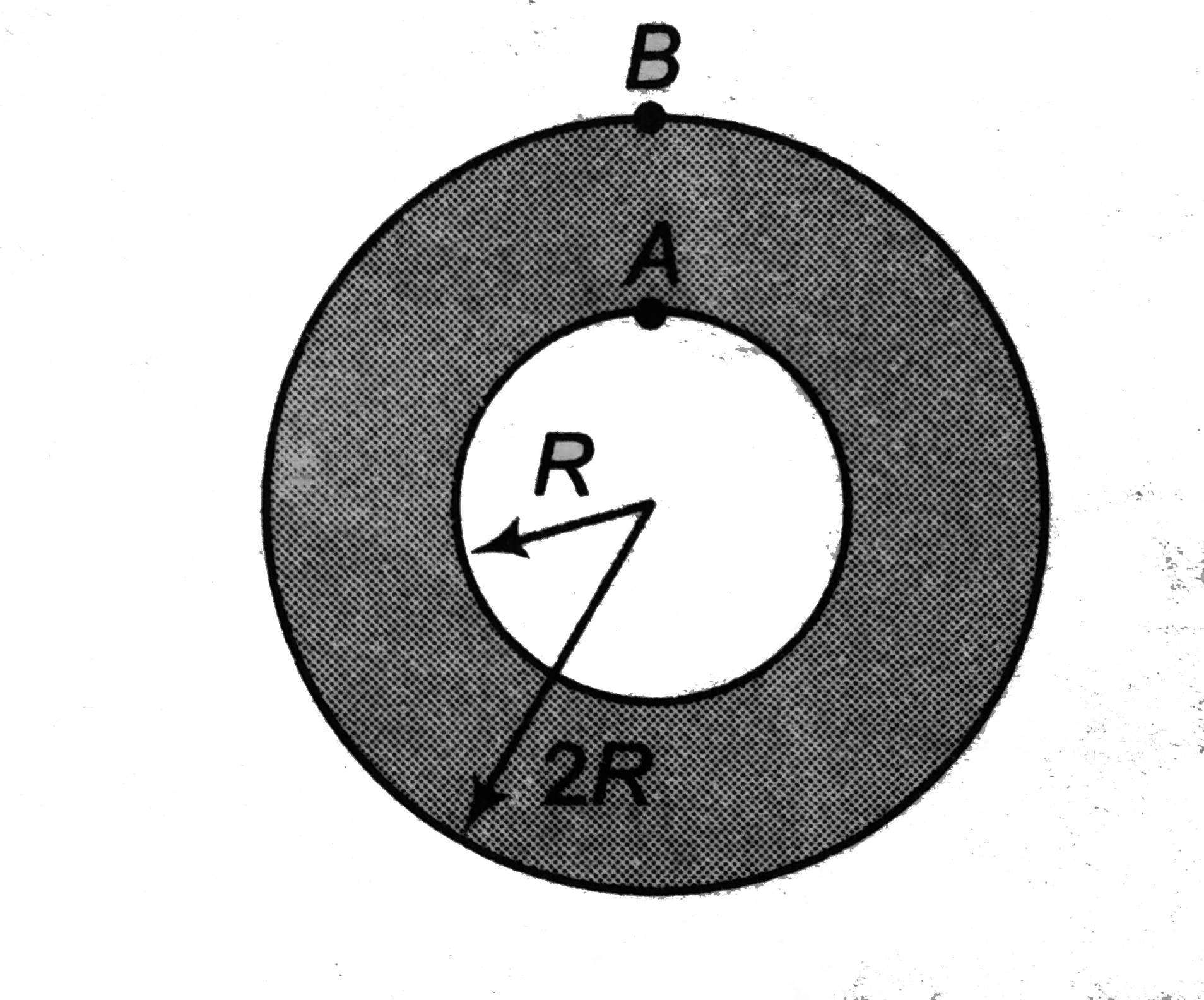
gA=gB (given)
then Gm1R2=Gm1+m2(2R)2
∴4m1=(m1+m2)
or 4{43πR3ρ1}=43πR3.ρ1
+{43π(2R)3−43πR3}ρ2
∴4ρ1=ρ1+7ρ2
∴ρ1ρ2=73
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.1
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
The density of the core of a planet is x and that of outer shell is y. The radii of the core and that of the planet are R and 2R. The acceleration due to gravity at the surface of planet is same as at a depth R. The ratio of x and y is n/3. Find the value of n.
View SolutionThe acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
View Solution
Knowledge Check
The radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2.The ratio of the accelerations due to gravity at their surface is
AR1ρ2R2ρ1BR1ρ1R2ρ2Cρ1R22ρ2R21DR1R2ρ1ρ2
A planet is made of two materials of density ρ1 and ρ2 as shown in figure. The acceleration due to gravity at surface of planet is same as a depth 'R'. The ratio of ρ1ρ2 is x3. Find the value of x.

View SolutionTwo planets A and B have the same averge density . Their radii RAandRB are such that RA:RB=3:1. If gA and gB are the acceleration due to gravity at the surfaces of the planets, the gA:gB equals
View SolutionTwo planets A and B have the same average density . Their radii RAandRB are such that RA:RB=3:1 . If gAandgB are the acceleration due to gravity at the surface of the planets , the gA:gB equals
View SolutionTwo planets of radii in the ratio 2:3 are made from the materials of density in the ratio 3:2. Then the ratio of acceleration due to gravity g1/g2 at the surface of two planets will be
View SolutionThe density of a newly discovered planet is twice that of earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the earth. If the radius of the earth is R, the radius of the planet would be
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
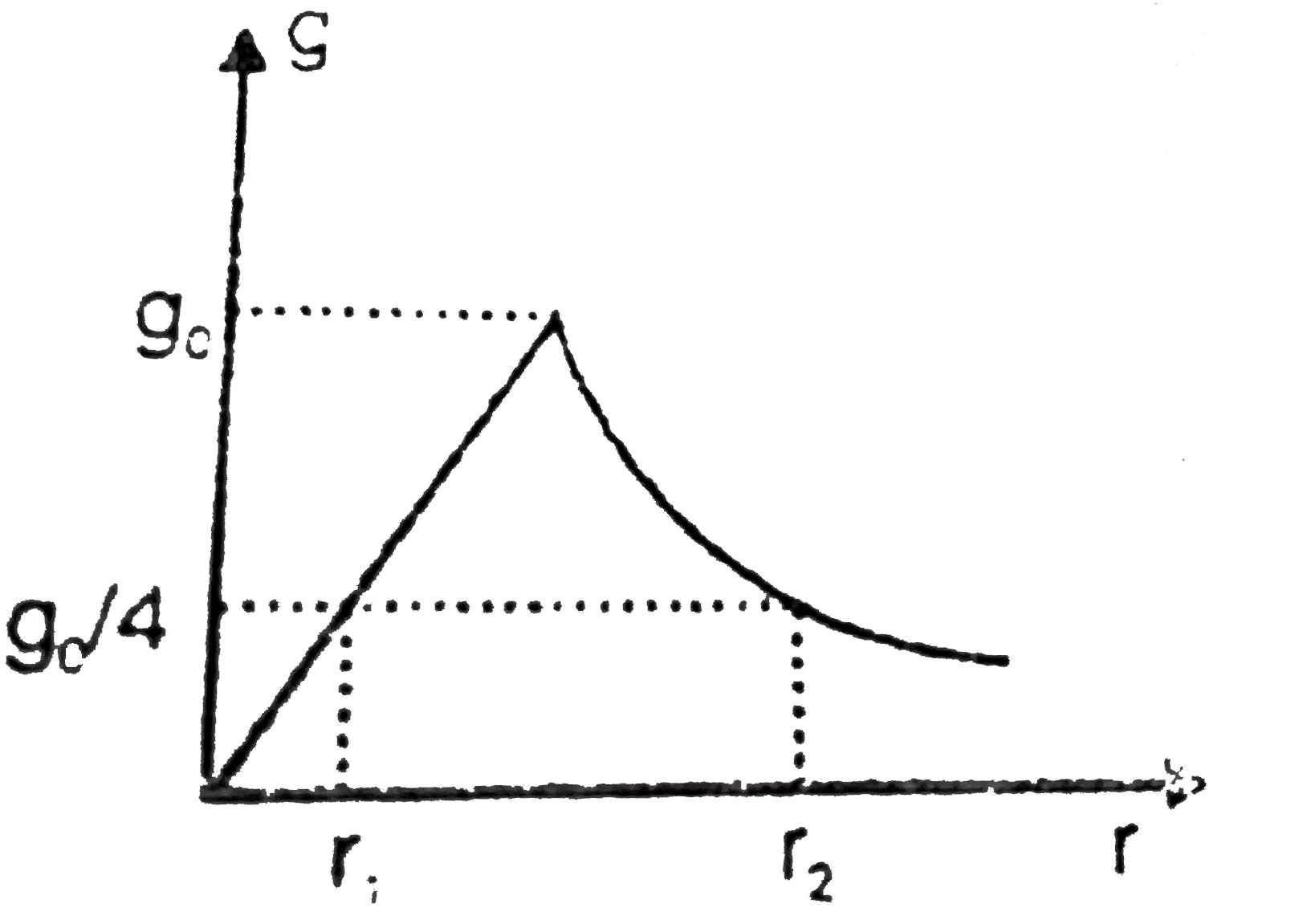
View SolutionThe radius of a planet is R. A satellite revolves around it in a circle of radius r with angular velocity ω0. The acceleration due to the gravity on planet's surface is
View Solution
