The distance travelled by a particle is proportional to the squares of time, then the particle travels with
uniform acceleration
uniform velocity
Both of these
speed changes
The correct Answer is:A
To solve the problem, we need to analyze the relationship between distance, time, velocity, and acceleration based on the information given in the question.
1. Understanding the Relationship:
The problem states that the distance s traveled by a particle is proportional to the square of time t. Mathematically, we can express this as:
s∝t2
This means that there exists a constant k such that:
s=kt2
2. Finding Velocity:
Velocity v is defined as the rate of change of distance with respect to time. We can find the velocity by differentiating the distance equation with respect to time:
v=dsdt=ddt(kt2)
Using the power rule of differentiation, we get:
v=k⋅2t=2kt
This shows that velocity v is directly proportional to time t.
3. Analyzing Velocity:
Since v=2kt, we can see that as time increases, velocity also increases. This indicates that the particle does not travel with uniform velocity.
4. Finding Acceleration:
Acceleration a is defined as the rate of change of velocity with respect to time. We can find the acceleration by differentiating the velocity equation with respect to time:
a=dvdt=ddt(2kt)
Differentiating gives:
a=2k
Here, 2k is a constant, indicating that the acceleration is uniform.
5. Conclusion:
Based on the analysis:
- The particle travels with uniform acceleration because the acceleration a=2k is constant.
- The velocity is not uniform since it changes with time.
Thus, the correct answer is that the particle travels with uniform acceleration.
The problem states that the distance s traveled by a particle is proportional to the square of time t. Mathematically, we can express this as:
s∝t2
This means that there exists a constant k such that:
s=kt2
Velocity v is defined as the rate of change of distance with respect to time. We can find the velocity by differentiating the distance equation with respect to time:
v=dsdt=ddt(kt2)
Using the power rule of differentiation, we get:
v=k⋅2t=2kt
This shows that velocity v is directly proportional to time t.
Since v=2kt, we can see that as time increases, velocity also increases. This indicates that the particle does not travel with uniform velocity.
Acceleration a is defined as the rate of change of velocity with respect to time. We can find the acceleration by differentiating the velocity equation with respect to time:
a=dvdt=ddt(2kt)
Differentiating gives:
a=2k
Here, 2k is a constant, indicating that the acceleration is uniform.
Based on the analysis:
- The particle travels with uniform acceleration because the acceleration a=2k is constant.
- The velocity is not uniform since it changes with time.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.5
25 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.6
20 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.3
10 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
The displacement of a particle starts from rest is proportional to the square of time, then the particle travels with
View SolutionThe distance travelled by a freely falling body is proportional to
View SolutionIn a straight line motion the distance travelled is proportional to the square root of the time taken The acceleration of the particle is proportional to :-
View SolutionA particle moves in one dimension from rest under the influence of a force that varies with the distance travelled by the particle as shown in the figure. The kinetic energy of the particle after it has travelled 3m is:
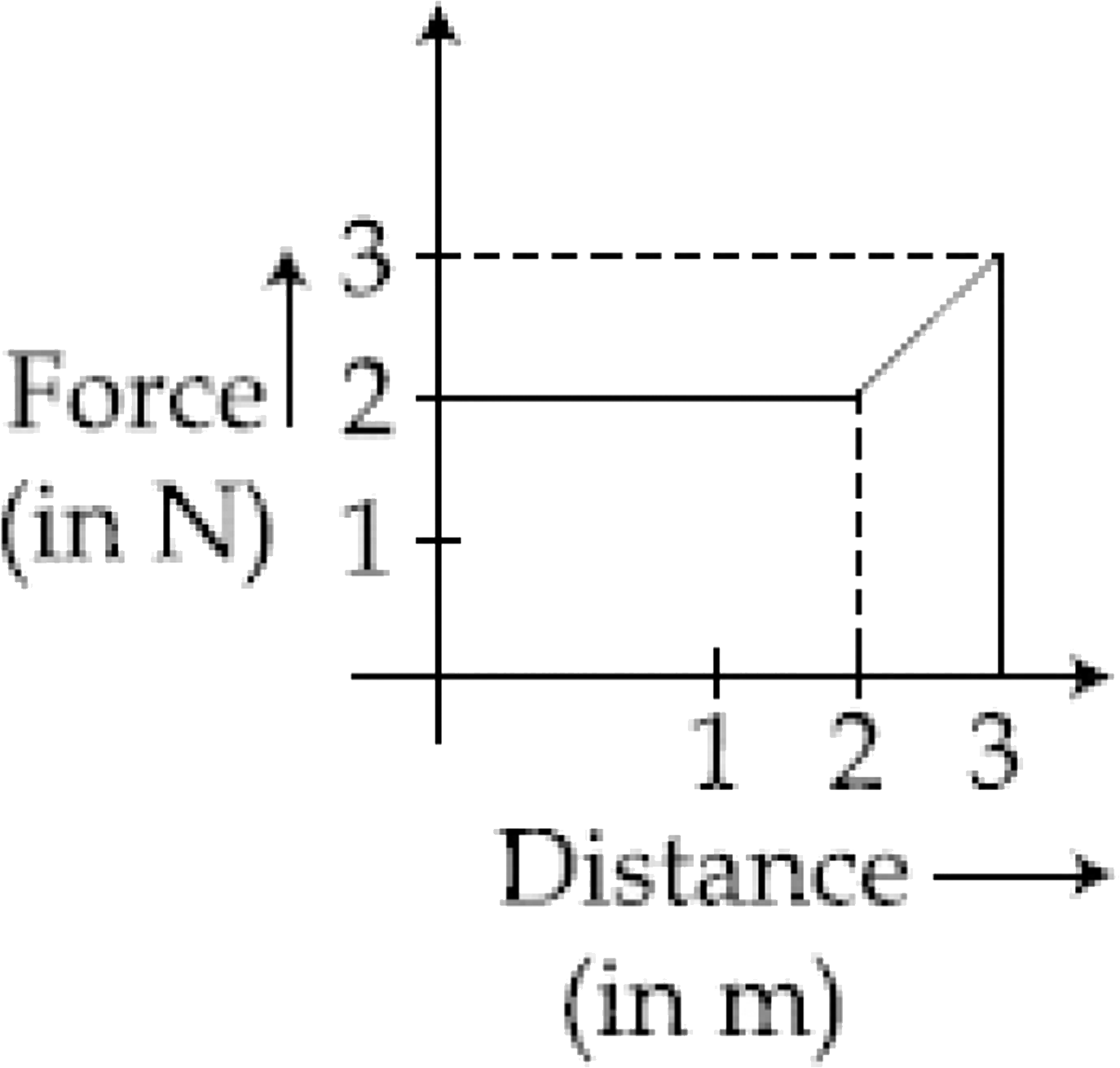
View SolutionName
Distance travelled in unit time
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionA particle is projected with velocity v0 along x - axis. The deceleration on the particle is proportional to the square of the distance from the origin i.e. a=−x2. The distance at which particle stops is -
View Solution(A):The displacement of a particle starting from rest is directly proportional to the cube of the time of travel then the particle is moving with non uniform acceleration.
(R ):Acceleration →a=d2→sdt2
View SolutionThe distance travelled by a particle starting from rest and moving with an acceleration 3ms−2, in the 5th second is.
View SolutionIf a particle is moving such that the velocity acquired is proportional to the square root of the distance covered, then its acceleration is
View Solution
