The flywheel of an engine, acted upon by a constant torque at the rate of 3000 rev/ min and develops a power of 10 kW. Find the torque acting on the wheel.
To find the torque acting on the flywheel, we will use the relationship between power, torque, and angular velocity. The formula we will use is:
P=τ⋅ω
Where:
- P is the power in watts (W)
- τ is the torque in newton-meters (N·m)
- ω is the angular velocity in radians per second (rad/s)
1. Convert Power to Watts:
The power given is 10 kW. We need to convert this to watts:
P=10 kW=10×103 W=10,000 W
2. Convert Revolutions per Minute to Radians per Second:
The flywheel rotates at 3000 revolutions per minute (rev/min). To convert this to radians per second (rad/s), we use the conversion factor:
ω=2π⋅n
where n is the number of revolutions per second. First, convert rev/min to rev/s:
n=3000 rev/min60 s/min=50 rev/s
Now, calculate ω:
ω=2π⋅50 rev/s=100π rad/s
3. Calculate Torque:
Rearranging the power formula to solve for torque gives:
τ=Pω
Substitute the values we have:
τ=10,000 W100π rad/s=10,000100⋅3.14≈10,000314≈31.83 N⋅m
4. Final Answer:
The torque acting on the wheel is approximately:
τ≈31.83 N⋅m
- P is the power in watts (W)
- τ is the torque in newton-meters (N·m)
- ω is the angular velocity in radians per second (rad/s)
The power given is 10 kW. We need to convert this to watts:
P=10 kW=10×103 W=10,000 W
The flywheel rotates at 3000 revolutions per minute (rev/min). To convert this to radians per second (rad/s), we use the conversion factor:
ω=2π⋅n
where n is the number of revolutions per second. First, convert rev/min to rev/s:
n=3000 rev/min60 s/min=50 rev/s
Now, calculate ω:
ω=2π⋅50 rev/s=100π rad/s
Rearranging the power formula to solve for torque gives:
τ=Pω
Substitute the values we have:
τ=10,000 W100π rad/s=10,000100⋅3.14≈10,000314≈31.83 N⋅m
The torque acting on the wheel is approximately:
τ≈31.83 N⋅m
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
11 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
If a constant torque acts on a body, the body?
View SolutionA flywheel of mass 100 kg and radius 1 m is rotating at the rate of 420 rev/min. Find the constant retarding torque to stop the wheel in 14 revolutions, the mass is concentrated at the rim. M.I. of the flywheel about its axis of rotation I=mr2.
View Solution
Knowledge Check
A rigid rod of length 2L is acted upon by some forces. All forces labelled F have the same magnitude. Which cases have a non-zero net torque acting on the rod about its centre ?
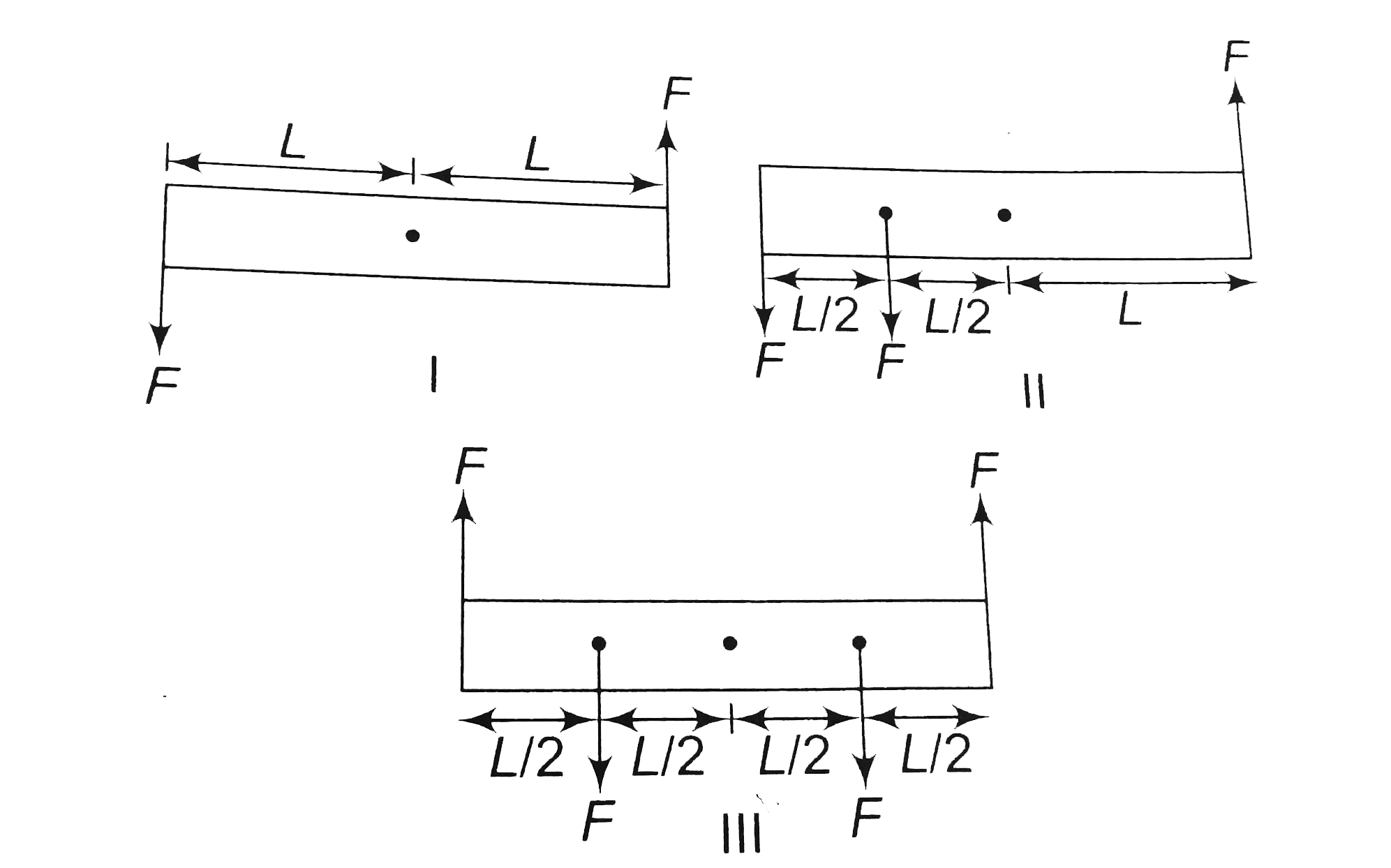 .AI and II onlyBII and III onlyCI and III onlyDThe net torque is zero in all cases.
.AI and II onlyBII and III onlyCI and III onlyDThe net torque is zero in all cases.
A magnetic of magnetic moment placed along the X-axis in an magnet field .Find the torque acting on the magnetic field
View SolutionA loop, carring a current i, lying in the plane of the paper, is in the field of a long straight wire with current i0 (inward) as shown in Fig. Find the torque acting on the loop.

View SolutionA circular coil of 20turns and radius 10cm carries a current of 5A. It is placed in a uniform magnetic field of 0⋅10T. Find the torque acting on the coil when the magnetic field is applied (a) normal to the plane of the coil (b) in the plane of coil. Also find out the total force acting on the coil.
View SolutionA dipolo is placed in the field of a point charge, the distance between the dipole and the field source being much greater than the dipole separation. Find the force acting on the dipole and the torque, if the dipole is arranged:
perpendicular to the line of force.
View SolutionA dipole is placed in the field of a point charge, the distance between the dipole and the field source being much greater than the dipole separation. Find the force acting on the dipole and the torque, if the dipole is arranged:
In the direction of the line of force.
View SolutionPoint C is the centre of mass of the rigid body shown in figure. Find the total torque acting on the body about point C.

View SolutionFigure shows a bent coil with all edges of length 1m and carrying a current 1 A.
a. Find the magnetic moment of the loop.
b. Find the torque acting on the loop.

View Solution
