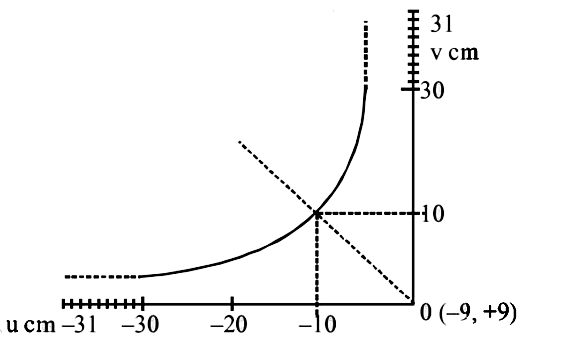
The following graph depicts the inverse of magnification versus the distance between the object and lens data for a setup. The focal length of the lens used in the setup is

250 m
0.004 m
125 m
0.002 m
The correct Answer is:B
Magnification (m) =+vu
From lens formula,
1v−1u=1f)⇒uv−1=uf⇒uv=uf+1
∴ graph between (uv) [ inverse of magnification] and u will be straight line with slope 1f
From graph, slope = 250
∴f=1250m=0.004m
Topper's Solved these Questions
Similar Questions
Knowledge Check
A concave lens forms the image of an object such that the distance between the object and image is focal length of the lens will be
A−6.2cmB−4.4cmC−8.6cmD−10cmIf the focal length of the objective lens is increased then
AMagnifying power of microscope will increase but that of telescope will decreaseBMagnifying power of microscope and telescope both will increaseCMagnifying power of microscope and telescope both will decreaseDMagnifying power of microscope will decrease but that of telescope will increaseIf the focal length of the objective lens is increased then
AMagnifying power of the microscope will increase but that of telescope will decreaseBMagnifying power of microscope and telescope both will increaseCMagnifying power of microscope and telescope both will decreaseDMagnifying power of microscope will decrease but that of telescope will increase
An object is placed at a distance u from an equiconvex lens such that the distannce between the object and its real image is minimum. The focal length of the lens is f. The value of u is
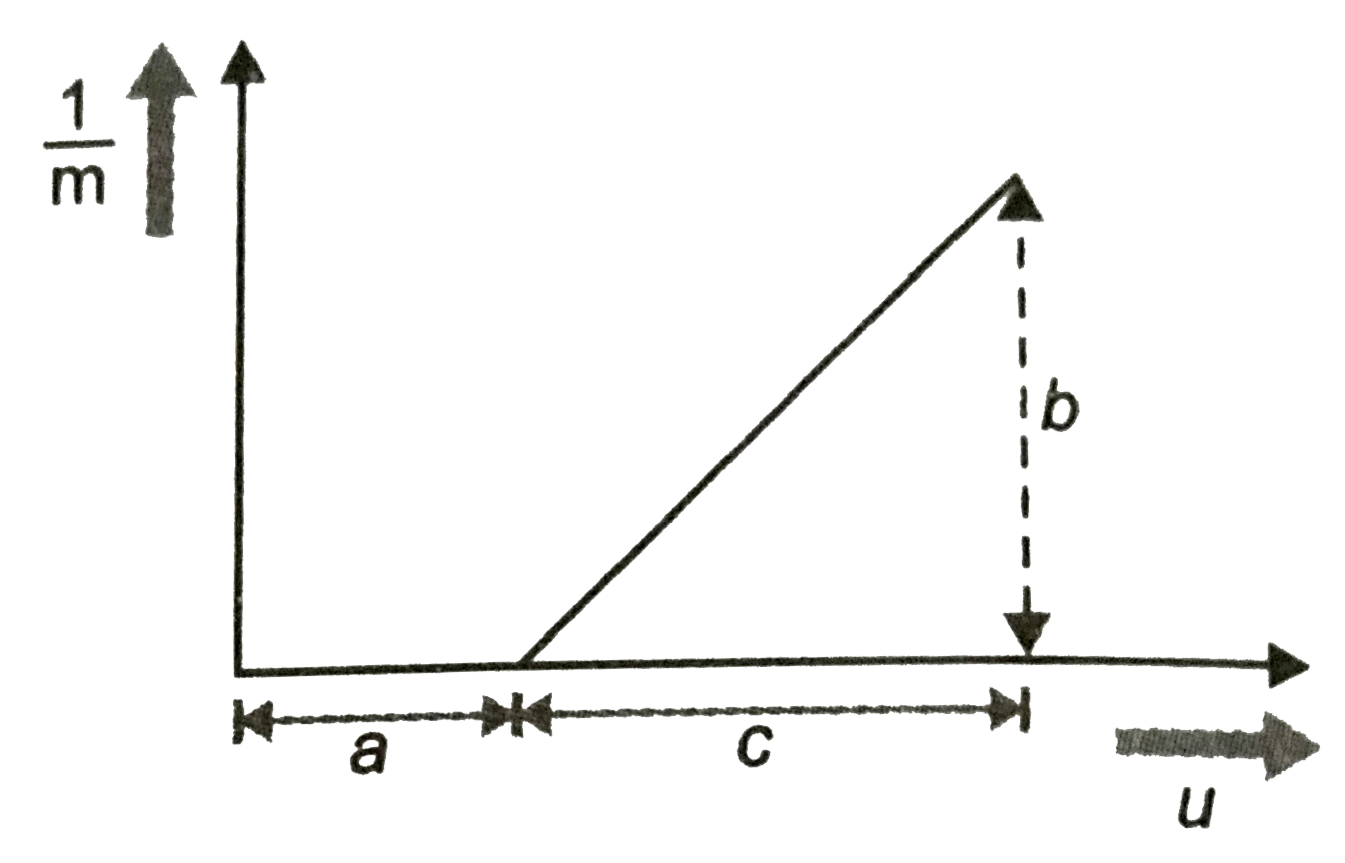
View SolutionThe graph in Fig. shows how the inverse of magnification 1/m produced by a convex thin lens varies with object distance u. What was the focal length of the lens used ?
 .
.
View Solution
The graps shows the variation of magnification m produced by as convex lens with the image distance v. The focal length of the lens is
View SolutionA cocave lens forms the image of an object such that the distance between the object and image is 10 cm and the magnification produced is 1/4. the focal length of the lens will be
View SolutionA concave lens forms the image of an object such that the distance between the object and image is 10cm and the magnification produced is 1/4. The focal length of the lens will be
View Solution