The force acting on a particle moving along X-axis is F=−k(x−v0t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks the particle . What kind of motion does he find for the particle?
To analyze the motion of the particle as observed by an observer moving at a constant velocity v0, we start with the given force equation:
F=−k(x−v0t)
where k is a positive constant.
Step 1: Rewrite the Force Equation
We can rewrite the force equation as:
F=−kx+kv0t
This equation consists of two terms: the first term −kx is dependent on the displacement x, and the second term kv0t is dependent on time t.
Step 2: Analyze the Terms
- The term −kx indicates a restoring force that is proportional to the displacement from the origin, which is characteristic of simple harmonic motion (SHM).
- The term kv0t is a linear function of time, which means it increases indefinitely as time progresses.
Step 3: Determine the Nature of the Motion
Since the second term kv0t is positive and increases with time, it implies that the force acting on the particle does not remain constant. Instead, it increases over time, which means the particle will not oscillate around an equilibrium position.
Step 4: Conclusion
Thus, the force acting on the particle does not represent simple harmonic motion because the force is not solely dependent on the displacement from an equilibrium position; it also has a time-dependent component that causes the force to increase indefinitely. Therefore, the observer moving with velocity v0 will find that the particle does not exhibit simple harmonic motion.
Final Answer
The motion observed by the observer is not simple harmonic motion due to the presence of the time-dependent term in the force equation.
---
We can rewrite the force equation as:
- The term −kx indicates a restoring force that is proportional to the displacement from the origin, which is characteristic of simple harmonic motion (SHM).
- The term kv0t is a linear function of time, which means it increases indefinitely as time progresses.
Since the second term kv0t is positive and increases with time, it implies that the force acting on the particle does not remain constant. Instead, it increases over time, which means the particle will not oscillate around an equilibrium position.
Thus, the force acting on the particle does not represent simple harmonic motion because the force is not solely dependent on the displacement from an equilibrium position; it also has a time-dependent component that causes the force to increase indefinitely. Therefore, the observer moving with velocity v0 will find that the particle does not exhibit simple harmonic motion.
The motion observed by the observer is not simple harmonic motion due to the presence of the time-dependent term in the force equation.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
A force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
View SolutionSTATEMENT -1 :The force acting on a particle moving alongx -axis is F=−α(x+vt), where α is a constant.
and
STATEMENT-2 : To an observer moving along x-axis with constant velocity v, it represents SHM.
View SolutionForce acting on a particle moving along x-axis as shown in figure. Find points of stable and unstable equlibrium.
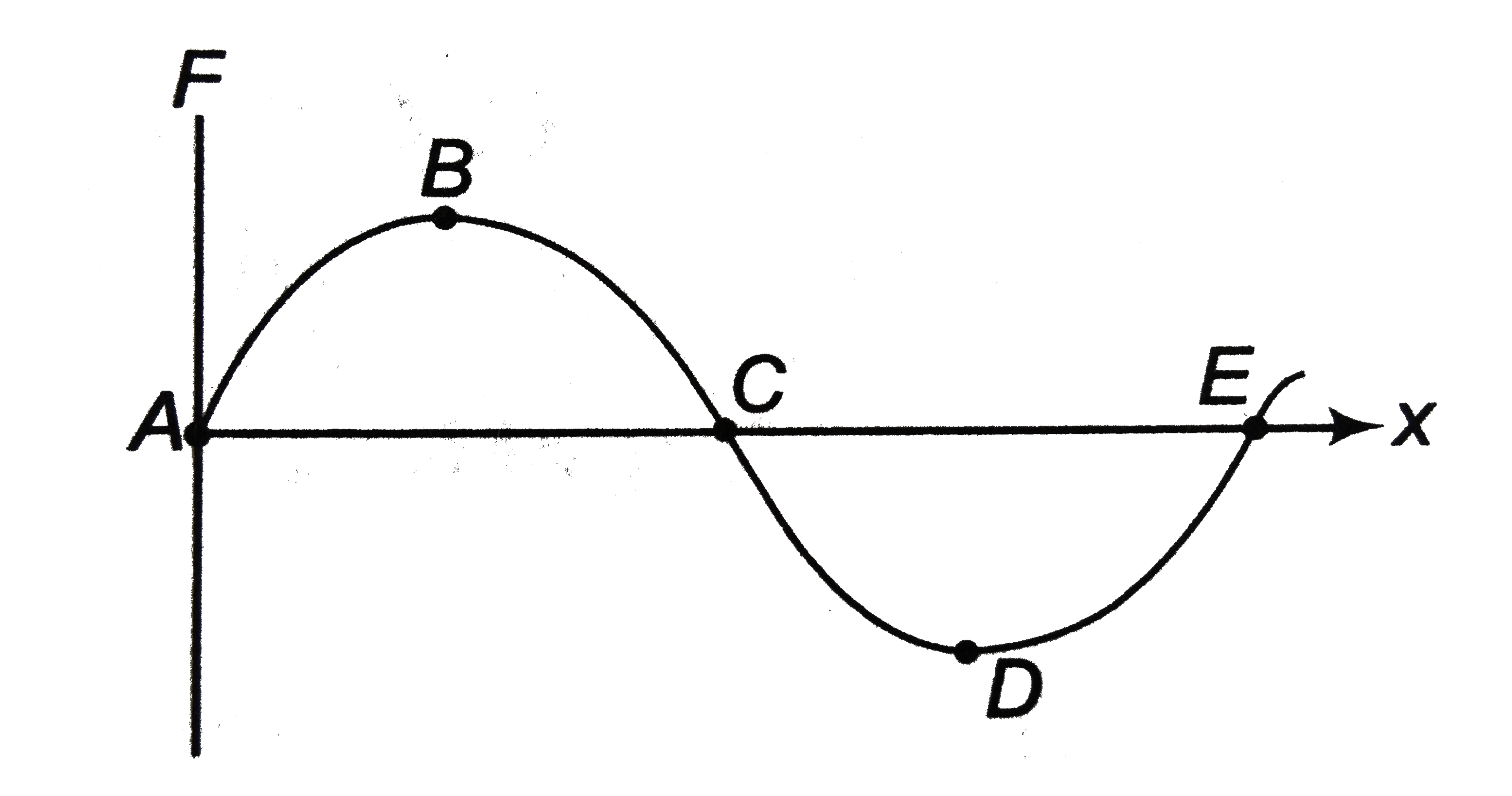 .
.
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionA particle moves along a path y=ax2 (where a is constant) in such a way that x-component of its velocity (ux) remains constant. The acceleration of the particle is
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V-t graph.
View SolutionThe magnitude of force acting on a particle moving along x-axis varies with time (t) as shown in figure. If at t = 0 the velocity of particle is v0, then its velocity at t=T0 will be

View SolutionA time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionThe position x of particle moving along x-axis varies with time t as x=Asin(ωt) where A and ω are positive constants. The acceleration a of particle varies with its position (x) as
View SolutionThe force acting on a body moving along x -axis varies with the position of the particle as shown in the fig. The body is in stable equilibrium at.
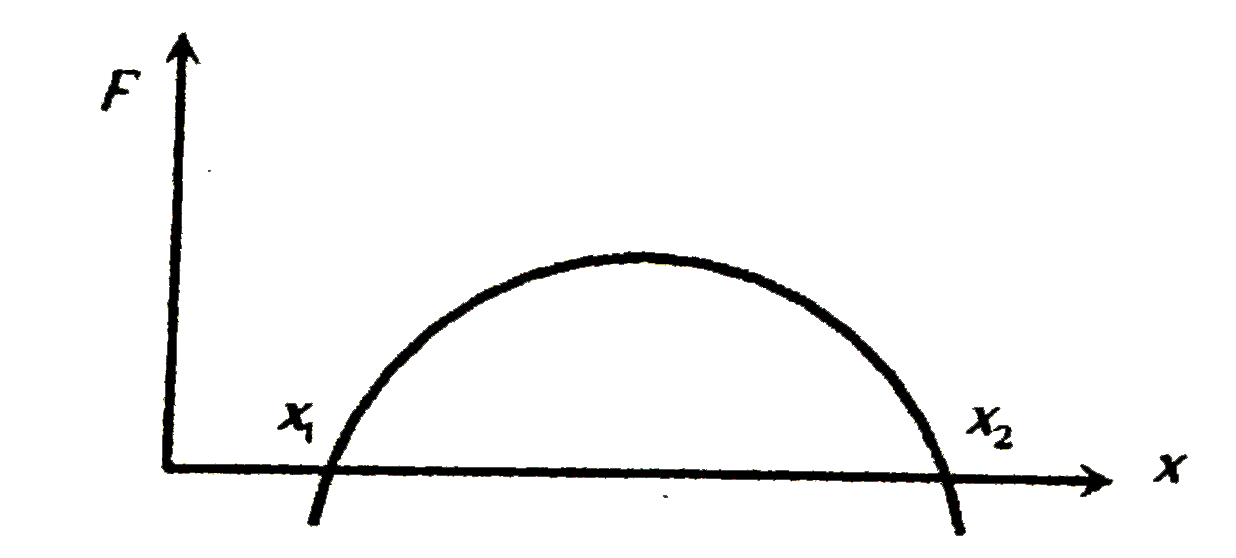
View Solution
