The force required to just move a body up the inclined plane is double the force required to just prevent the body from sliding down the plane. The coefficient of friction is μ. If θ is the angle of inclination of the plane than tanθ is equal to
(a)μ
(b)3μ
(c)2μ
(d)0.5μ
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on a body on an inclined plane and derive the relationship between the angle of inclination (θ) and the coefficient of friction (μ). Here’s the step-by-step solution:
Step 1: Understand the Forces Acting on the Body
When a body is placed on an inclined plane, the forces acting on it include:
- The weight of the body (mg), acting downwards.
- The normal force (N), acting perpendicular to the inclined surface.
- The frictional force (f), which can act either up or down the incline depending on the situation.
Step 2: Identify the Two Scenarios
1. Force to Move the Body Upwards (F1): This force must overcome both the component of gravitational force acting down the incline (mg sin θ) and the frictional force acting downwards.
2. Force to Prevent Sliding Down (F2): This force must balance the component of gravitational force acting down the incline (mg sin θ) and the frictional force acting upwards.
Step 3: Establish Relationships
From the problem, we know:
- F1=2F2
For F1 (Force to move up):
The equation can be written as:
F1=f+mgsinθ
Where the frictional force f=μN and N=mgcosθ. Thus:
f=μmgcosθ
So,
F1=μmgcosθ+mgsinθ
For F2 (Force to prevent sliding):
The equation can be written as:
F2=mgsinθ−f
Substituting for f:
F2=mgsinθ−μmgcosθ
Step 4: Substitute F2 into the F1 Equation
Now, substituting F2 into the equation F1=2F2:
μmgcosθ+mgsinθ=2(mgsinθ−μmgcosθ)
Step 5: Simplify the Equation
Expanding and simplifying:
μmgcosθ+mgsinθ=2mgsinθ−2μmgcosθ
Rearranging gives:
μmgcosθ+2μmgcosθ=2mgsinθ−mgsinθ
This simplifies to:
3μmgcosθ=mgsinθ
Step 6: Divide by mg
Dividing through by mg (assuming mg ≠ 0):
3μcosθ=sinθ
Step 7: Rearranging to Find tan θ
Dividing both sides by cosθ:
3μ=tanθ
Conclusion
Thus, we find:
tanθ=3μ
Final Answer
The value of tanθ is equal to 3μ.
---
When a body is placed on an inclined plane, the forces acting on it include:
- The weight of the body (mg), acting downwards.
- The normal force (N), acting perpendicular to the inclined surface.
- The frictional force (f), which can act either up or down the incline depending on the situation.
1. Force to Move the Body Upwards (F1): This force must overcome both the component of gravitational force acting down the incline (mg sin θ) and the frictional force acting downwards.
2. Force to Prevent Sliding Down (F2): This force must balance the component of gravitational force acting down the incline (mg sin θ) and the frictional force acting upwards.
From the problem, we know:
- F1=2F2
The equation can be written as:
F1=f+mgsinθ
Where the frictional force f=μN and N=mgcosθ. Thus:
f=μmgcosθ
So,
F1=μmgcosθ+mgsinθ
The equation can be written as:
F2=mgsinθ−f
Substituting for f:
F2=mgsinθ−μmgcosθ
Now, substituting F2 into the equation F1=2F2:
μmgcosθ+mgsinθ=2(mgsinθ−μmgcosθ)
Expanding and simplifying:
μmgcosθ+mgsinθ=2mgsinθ−2μmgcosθ
Rearranging gives:
μmgcosθ+2μmgcosθ=2mgsinθ−mgsinθ
This simplifies to:
3μmgcosθ=mgsinθ
Dividing through by mg (assuming mg ≠ 0):
3μcosθ=sinθ
Dividing both sides by cosθ:
3μ=tanθ
Thus, we find:
tanθ=3μ
The value of tanθ is equal to 3μ.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A body of mass m is kept on an inclined plane . The force required to just move a body up the inclined plane is double the force required to just prevent the body from sliding down the plane. If the coefficient of friction is μ, what is the inclination of the plane ?
View SolutionThe force F1 required to just moving a body up an inclined plane is double the force F2 required to just prevent the body from sliding down the plane. The coefficient of friction is μ. The inclination θ of the plane is :
View SolutionThe force required to move a body up a rough inclined plane is double the force required to prevent the body from sliding down the plane. The coefficient of friction when the angle of inclination of the plane is 60∘ is .
View SolutionIn the situation shown, the force required to just move a body up an inclined plane is double the force required to just prevent the body from sliding down the plane. The coefficient of friction between the block and plane is μ. The angle of inclination of the plane from horizontal is given by :

View SolutionThe force required just to move a body up an inclined plane is double the force required just to prevent the body sliding down. If the coefficient of friction is 0.25, what is the angle of inclination of the plane ?
View SolutionThe minimum force required to move a body up an inclined plane is three times the minimum force required to prevent it from sliding down the plane. If the coefficient of friction between the body and the inclined plane is 12√3, the angle of the inclined plane is
View SolutionWhen a body slides down an inclined plane with coefficient of friction as μk, then its acceleration is given by .
View SolutionA block is pushed up a rough inclined plane of 45°. If the time of descent is twice the time of ascent, the coefficient of friction is
View SolutionA block has been placed on an inclined plane with the slope angle θ. Block slide down the plane at constant speed. The cofficient of Kinetic friction is equal to
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
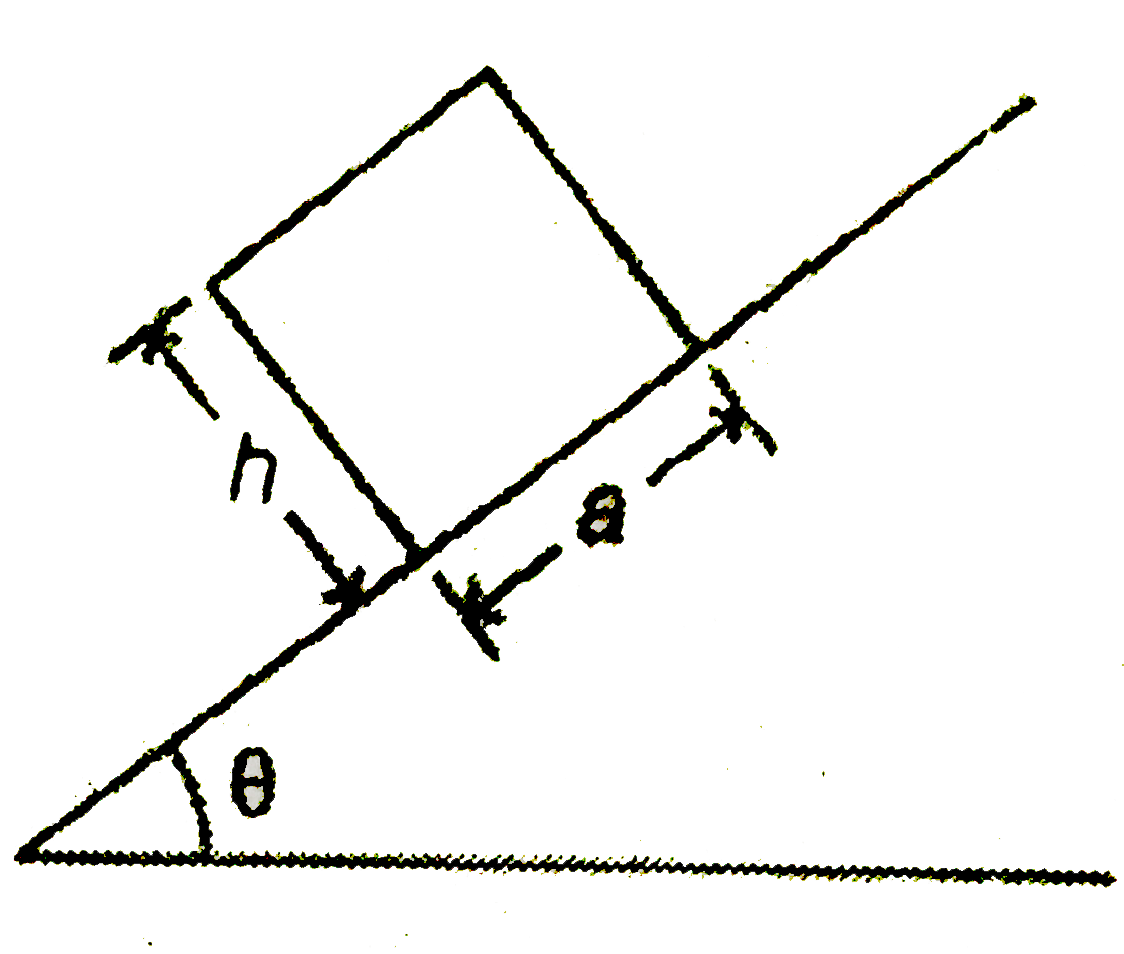
View Solution
