The time taken by a body to slide down a rough 45∘ inclined plane is twice that required to slide down a smooth 45∘ inclined plane. The coefficient of kinetic friction between the object and rough plane is given by
13
34
√34
√23
The correct Answer is:B
To solve the problem, we need to analyze the motion of a body sliding down both a smooth and a rough inclined plane at an angle of 45∘. We will derive the coefficient of kinetic friction between the object and the rough plane based on the given information.
1. Understanding the Problem:
- We have two inclined planes: one smooth and one rough, both inclined at an angle of 45∘.
- The time taken to slide down the rough plane (t1) is twice that of the smooth plane (t2):
t1=2t2
2. Setting Up the Forces:
- For the smooth inclined plane, the only force causing acceleration is the component of gravity along the incline:
Fsmooth=mgsin(45∘)=mg⋅1√2
- The acceleration (a2) on the smooth plane is:
a2=gsin(45∘)=g⋅1√2
3. For the Rough Inclined Plane:
- On the rough inclined plane, the forces acting on the body include the gravitational component down the incline and the frictional force opposing the motion:
Frough=mgsin(45∘)−fk
- The frictional force fk is given by:
fk=μmgcos(45∘)=μmg⋅1√2
- Therefore, the net force on the rough plane is:
Fnet=mgsin(45∘)−μmgcos(45∘)=mg⋅1√2−μmg⋅1√2
- The acceleration (a1) on the rough plane is:
a1=Fnetm=g⋅1√2(1−μ)
4. Relating Time and Acceleration:
- The time taken to slide down an incline is inversely related to the square root of the acceleration:
t∝1√a
- Therefore, we can write:
t1t2=√a2a1
- Substituting the expressions for a1 and a2:
t1t2=
⎷g⋅1√2g⋅1√2(1−μ)=√11−μ
5. Substituting the Time Relation:
- Since t1=2t2, we substitute this into our equation:
2=√11−μ
- Squaring both sides gives:
4=11−μ
- Rearranging leads to:
1−μ=14
- Thus:
μ=1−14=34
6. Final Answer:
- The coefficient of kinetic friction between the object and the rough plane is:
μ=34
- We have two inclined planes: one smooth and one rough, both inclined at an angle of 45∘.
- The time taken to slide down the rough plane (t1) is twice that of the smooth plane (t2):
t1=2t2
- For the smooth inclined plane, the only force causing acceleration is the component of gravity along the incline:
Fsmooth=mgsin(45∘)=mg⋅1√2
- The acceleration (a2) on the smooth plane is:
a2=gsin(45∘)=g⋅1√2
- On the rough inclined plane, the forces acting on the body include the gravitational component down the incline and the frictional force opposing the motion:
Frough=mgsin(45∘)−fk
- The frictional force fk is given by:
fk=μmgcos(45∘)=μmg⋅1√2
- Therefore, the net force on the rough plane is:
Fnet=mgsin(45∘)−μmgcos(45∘)=mg⋅1√2−μmg⋅1√2
- The acceleration (a1) on the rough plane is:
a1=Fnetm=g⋅1√2(1−μ)
- The time taken to slide down an incline is inversely related to the square root of the acceleration:
t∝1√a
- Therefore, we can write:
t1t2=√a2a1
- Substituting the expressions for a1 and a2:
t1t2=
⎷g⋅1√2g⋅1√2(1−μ)=√11−μ
- Since t1=2t2, we substitute this into our equation:
2=√11−μ
- Squaring both sides gives:
4=11−μ
- Rearranging leads to:
1−μ=14
- Thus:
μ=1−14=34
- The coefficient of kinetic friction between the object and the rough plane is:
μ=34
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question32videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension9videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason28videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
A given object taken n time more time to slide down 45∘ rough inclined plane as it taken to slide down a perfectly smooth 45∘ incline The coefficient of kintic friction between the object and the incline is .
View SolutionA piece of ice slides down a 45∘ incline in twice the time it takes to slide down a frictionless 45∘ incline . What is the coefficient of friction between the ice and the incline ? .
View Solution
Knowledge Check
- Question 1 - Select One
Starting from rest, a body slides down a 45∘ inclined plane in twice the time it itakes to slide the same distance in the absence of friction.
They the coefficient of friction between the body and the inclined plane isA1/4B2/3C3/4D√3/2
An object takes 1 second to slide down a rough 45∘ inclined plane. The time taken to slide down a smooth 30∘ inclined plane having the same slope length is (μ=0.5)
View SolutionStarting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View SolutionTwo identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
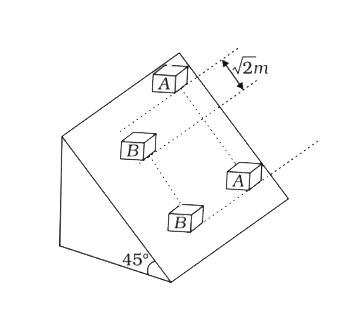 View Solution
View SolutionIn the case of a body sliding down a rough inclined plane show that μs=tanθ
View SolutionStarting from rest a body slides down a 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of the body and the inclined plane is :
View SolutionA block of mass m slides down a rough inclined plane with an acceleration g2
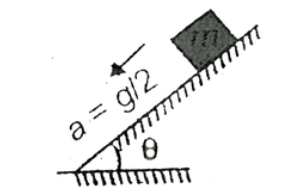 View Solution
View SolutionStarting from rest, the time taken by a body sliding down on a rough inclined plane at 45∘ with the horizontal is twice the time taken to travel on a smooth plane of same inclination and same distance. Then, the coefficient of kinetic friction is
View Solution

