The free damped oscillations are maintained in a circuit, such that the voltage across the capacitor varies as V=Vmθβtcosωt, Find the moments of time when the modulus of the voltage across the capacitor reaches
(a) peak values,
(b) maximum ( extremum ) values.
Given V=Vme−βtcosωt
(a) The phrase ' peak values ' is not clear. The answer is obtained on taking |cosωt|=1
i.e. t=πnω.
(b) For extrema dVdt=0
−βcosωt−ωsinωt=0
or tanωt=−β/ω
i.e. ωt=nπ+tan−1(−βω).
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Find how the voltage across the capacitor C varies with time t after closing of the switch Sw at the moment t=0.
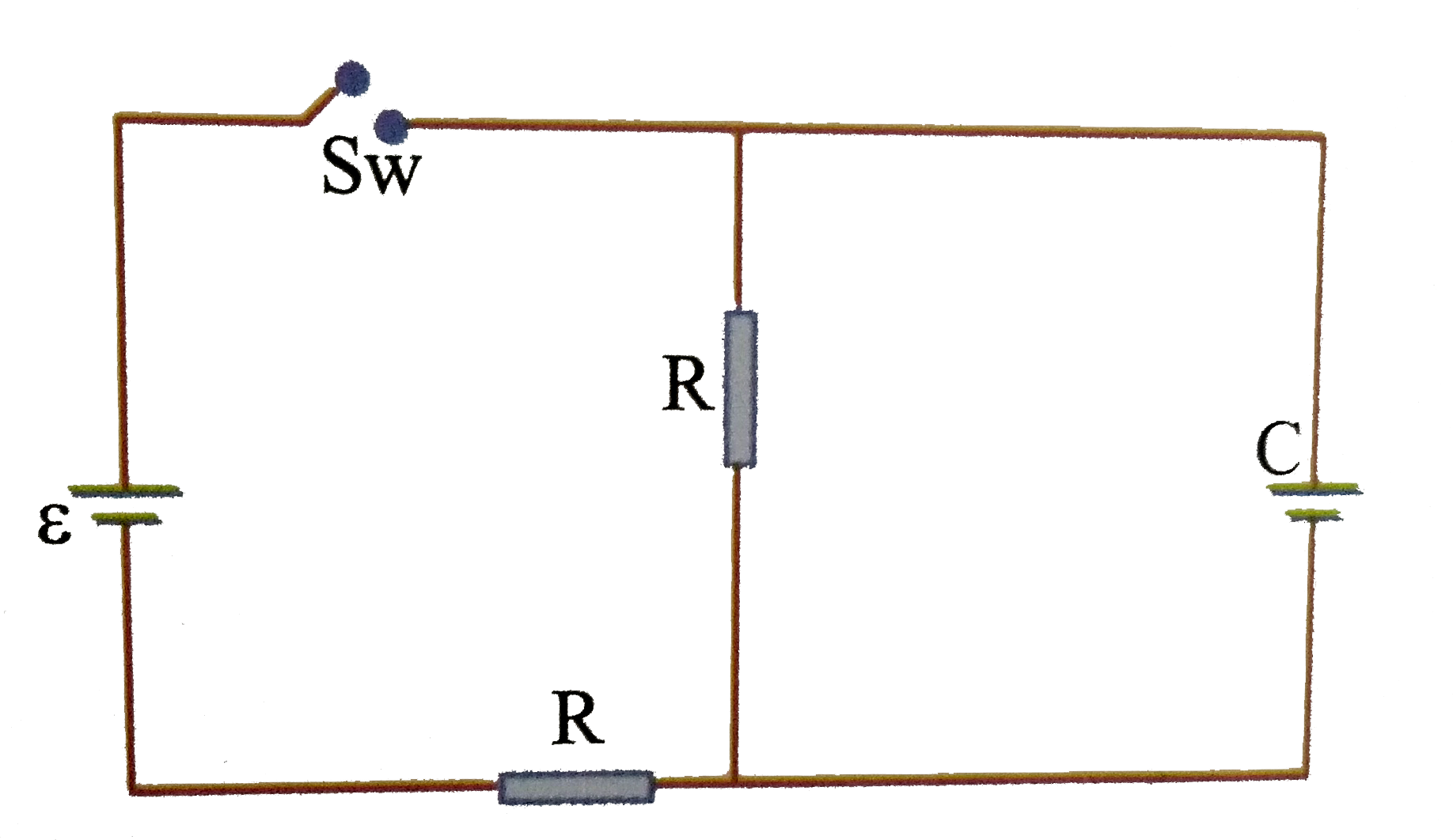 .
.
View SolutionA time varying voltage is applied to the clamps A and B such that voltage across the capacitor plates is as shown in the figure. Plot the time dependence of voltage across the terminals of the esistance E and D.
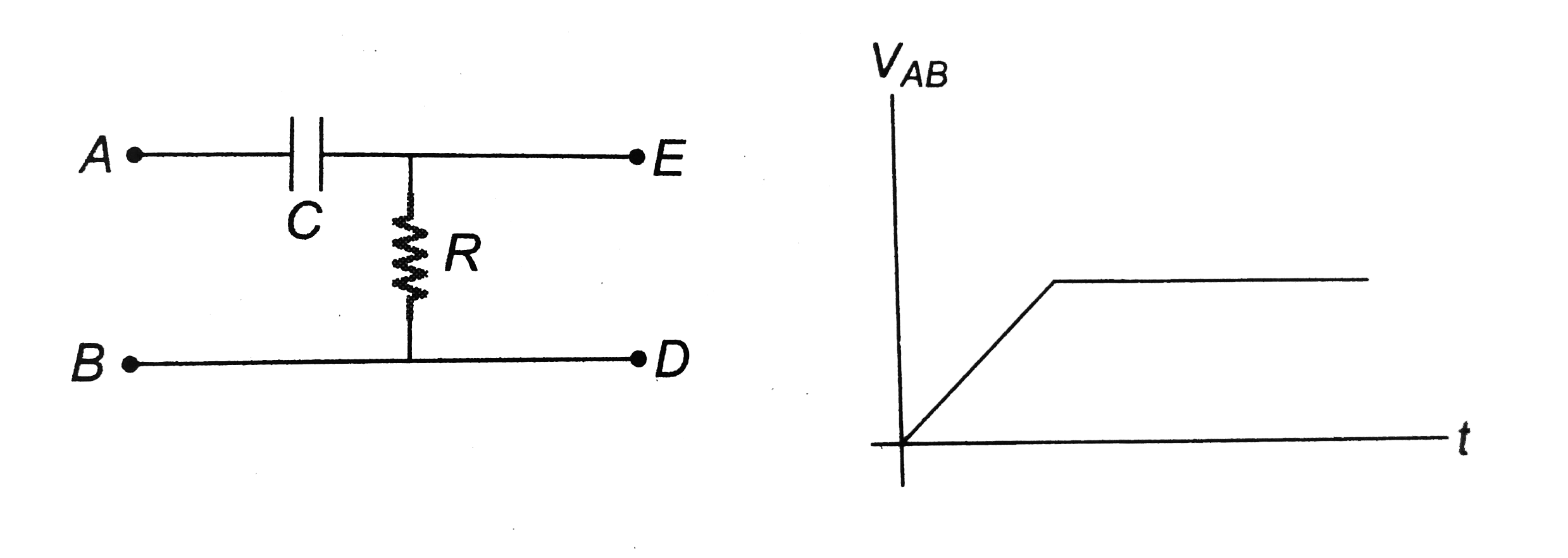
View Solution
Knowledge Check
Let q be the charge on the capacitor at any time t. The voltage V across the capacitor is
AVmsinωt=qCBVmcosωt=2VCCVmcosωt=q2CDVmsinωt=2qCIn the given circuit the R.M.S values of voltages across the capacitor C, inductor L and resistor R1 are 12V, 10V and 5 V respectively. Then the peak voltage across R2 is
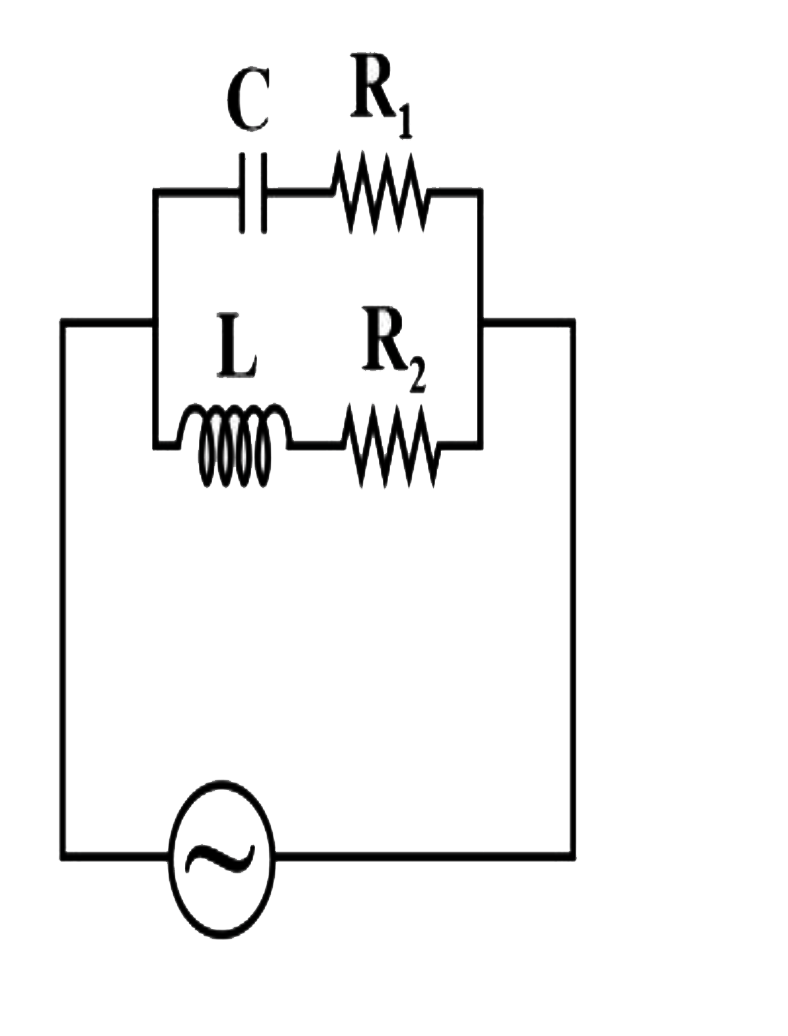 A7√2VB√69VC√138VDnone of these
A7√2VB√69VC√138VDnone of theseA circuit is shown below.
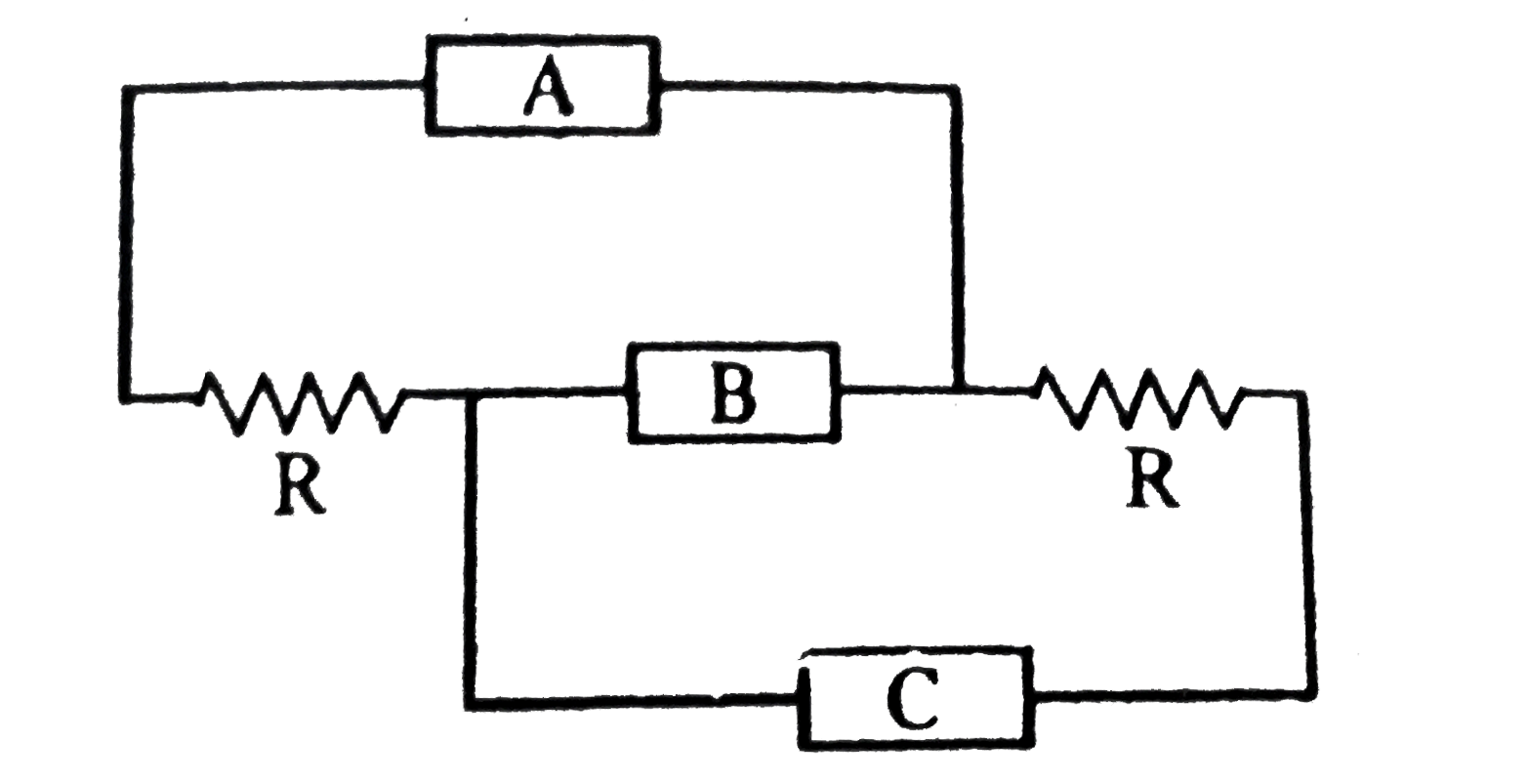
If A is a capacitor, B is an ideal ammeter and C is an ideal battery of voltage V, what is the voltage across the capacitor?AVBV2C2VD0
An oscillating circuit consisting of a capacitor with capacitance C and a coil of inductance L maintans free undamped oscillations with voltage amplitude across the capacitor equal to Vm. For an arbitrary moment of time find the relation between the current I in the circuit and the voltage V acroos the capacitor. Solve this problem usdini Ω's law and then the energy conservation law.
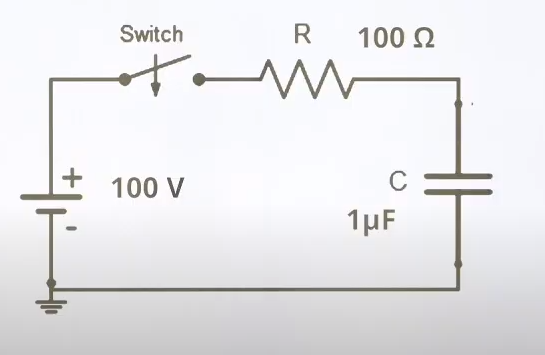
View SolutionThe switch is closed at t=0. Find time after which voltage across capacitor becomes 50 V. (take ln 2 = 0.6)
View SolutionA certain oscillating circuit consits of a capacitor with capacitance C, a coil with inductance L and active resistance R, and a switch . When the swith was disconnected, the capacitor was charged, then the switch was closed and oscillations set in. Find the ratio of the voltage across the capacitor to its peak value at the moment immediatel after closing the switch.
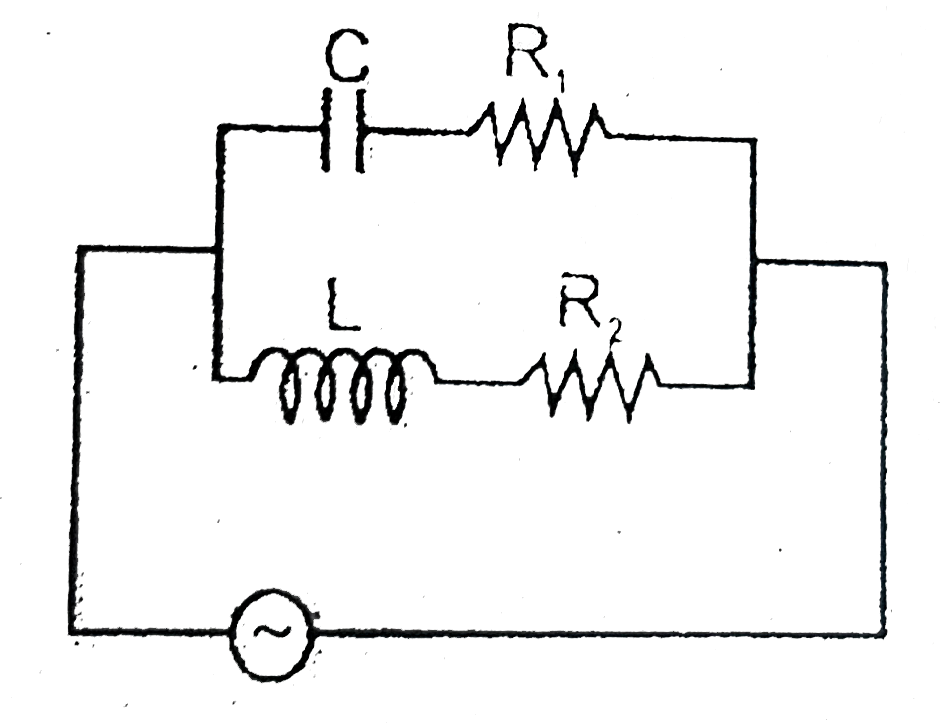
View SolutionIn the circuit the rms value of voltage across the capacitor C, inductor L and resister R1 are respectively 5√5V, 10 V and 5V. Then the peak voltage a cross R2 is
View SolutionIn a series L−C−R circuit, currenrt in the circuit is 11A when the applied voltage is 220V. voltage across the caspcitor is 200V. If the value of resistor is 20Ω, then the voltage across the unknown inductor is
View Solution
