The graph between the instantaneous concentration (N) of a radioactive element and time (t) is.
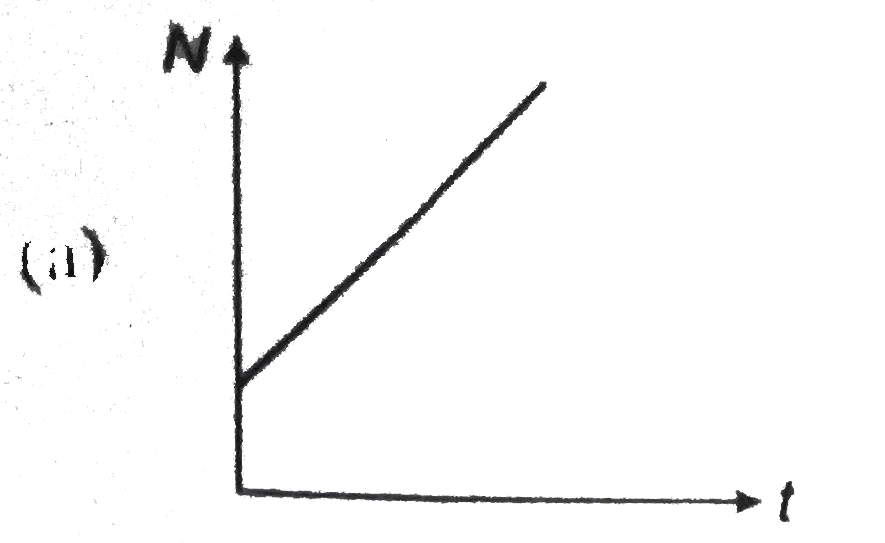
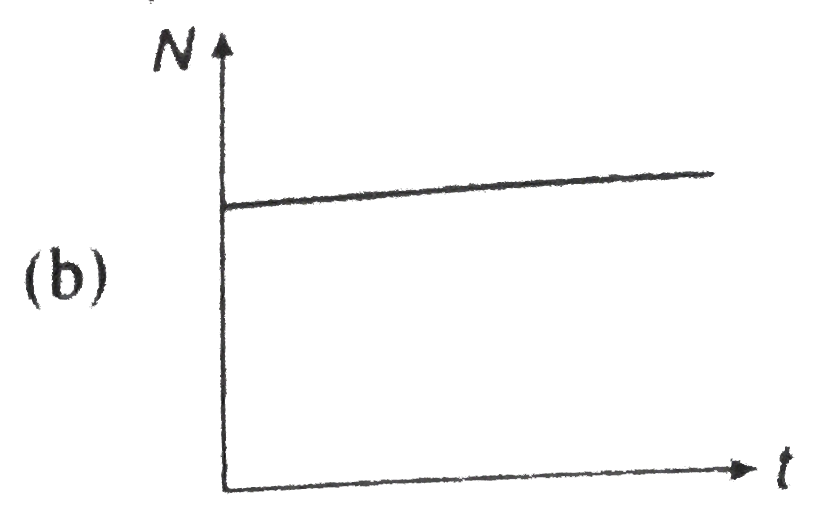
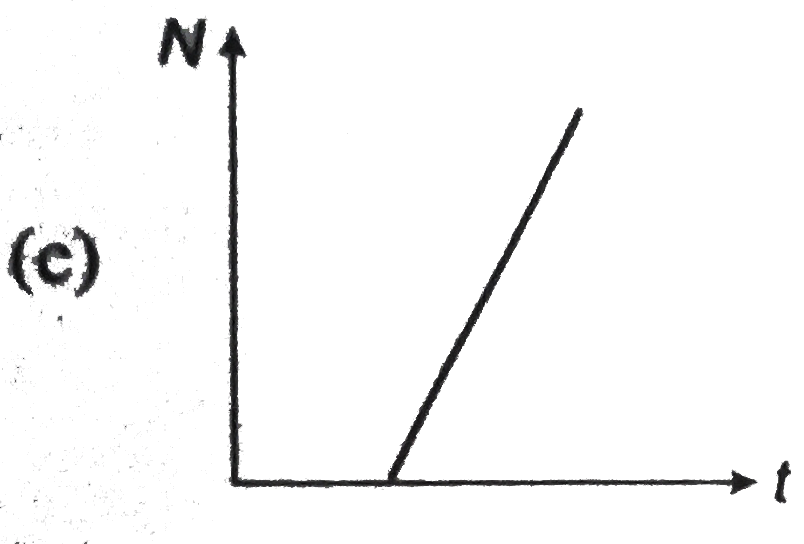
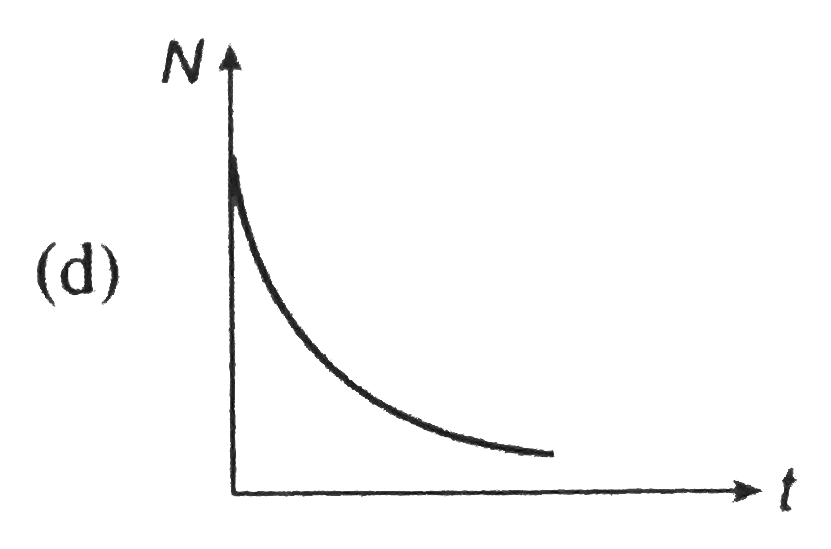
The correct Answer is:D
(d) By using N=N0e−λt and dNdt=−λN
It shows that N decreases exponentially with time.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - NUCLEAR PHYSICSEXERCISE - Problems Based On Mixed Concepts58videos
NUCLEAR PHYSICS
- BOOK - A2ZCHAPTER - NUCLEAR PHYSICSEXERCISE - Section B - Assertion Reasoning13videos
NUCLEAR PHYSICS
- BOOK - A2ZCHAPTER - NUCLEAR PHYSICSEXERCISE - Radioactivity42videos
NUCLEAR PHYSICS
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Mock Test 344videos
MOCK TEST
- BOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE29videos
SEMICONDUCTOR ELECTRONICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The graph between number of decayed atoms N' of a radioactive element and time t is.
A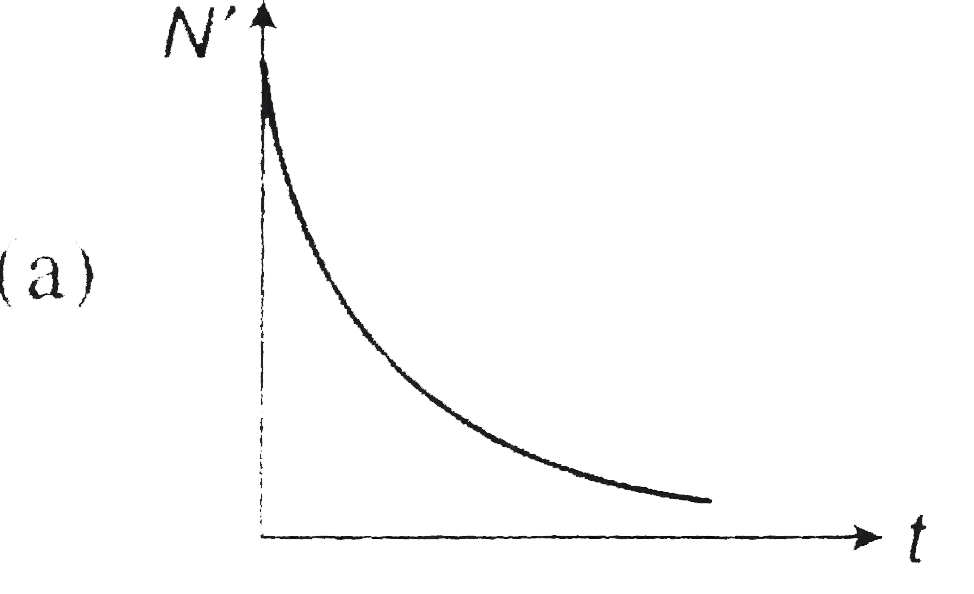 .B
.B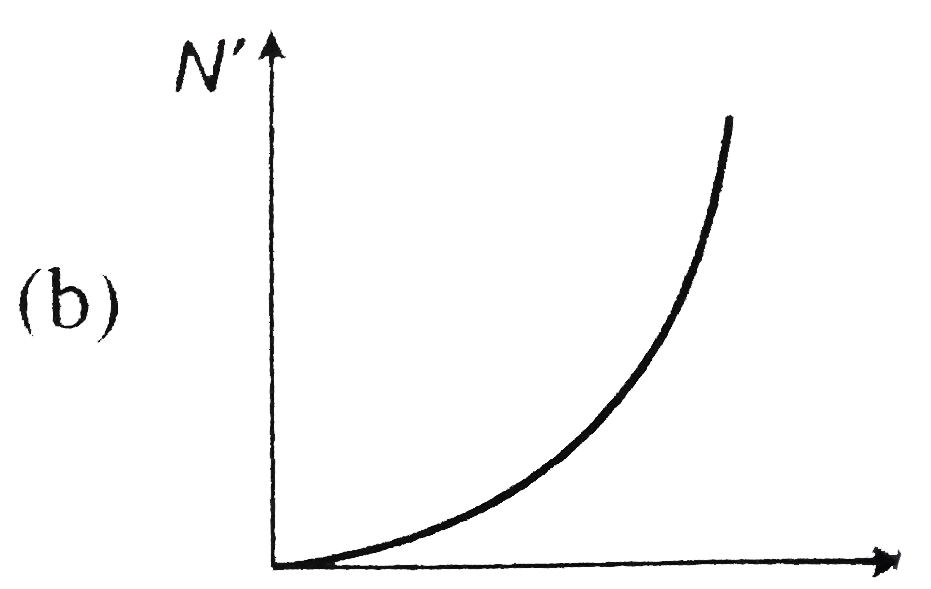 .C
.C .D
.D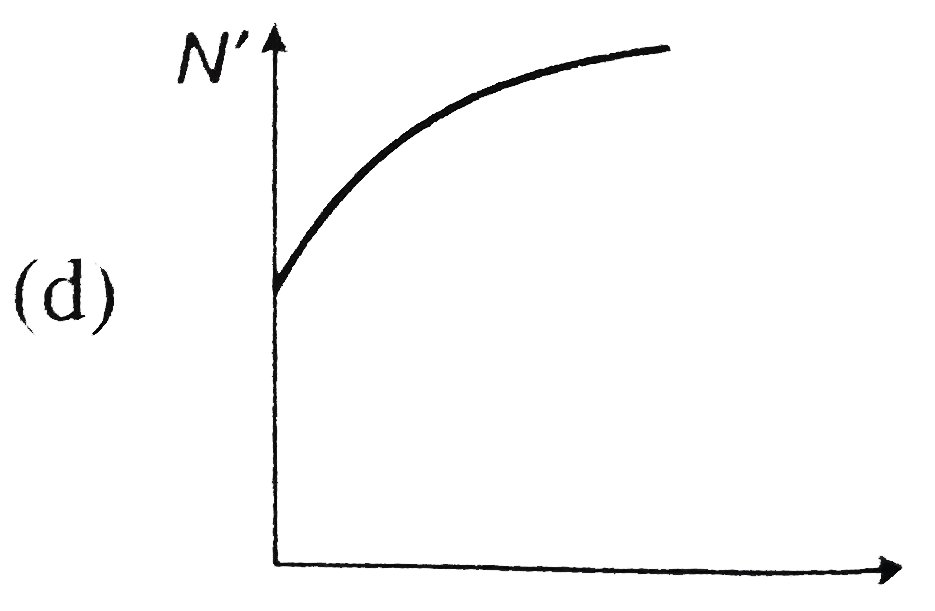 .
. - Question 2 - Select One
99% of a radioactive element will decay between
A6 and 7 half-livesB7 and 8 half-livesC8 and 9 half-livesD9 half-lives - Question 3 - Select One
The graph between instantaneous velocity and acceleration of a particle performing S.H.M. is
AparabolaBstraight lineCellipseDcircle
The graph between remaining radioactive atoms and time for a radioactive decay is
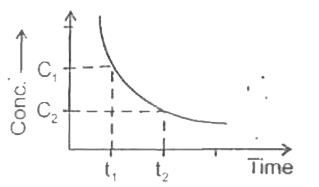
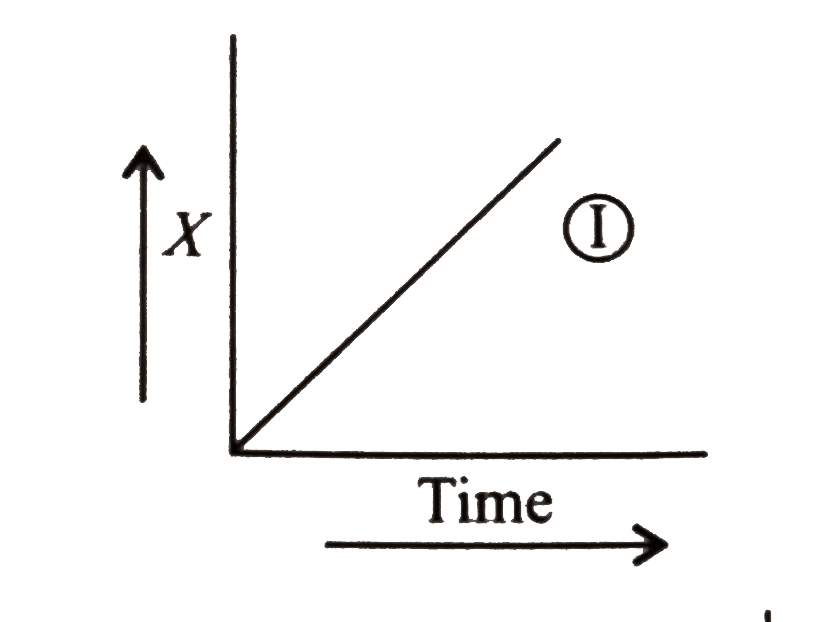
View SolutionThe graph between concentration (X) of the Product and time of the reaction A→B is of the type 1. Hence, graph between −d[A]dt and time will be of the type:
 View Solution
View SolutionThe graph shows how the count-rate A of a radioactive source varies with time t. A and t are related as: (assume in (12)=2.5)
 View Solution
View SolutionA radioactive sample decays to form a stable nuclide. A graph showing variation of rate of disintegration (dNdt) of radioactive sample with time (t) is
View SolutionFor the reactionA→B, for which graph between half life (t1/2)and∈itialconcentration(a)oftherectantisgivenbelow<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NRA_PHY_CHM_JMA_C07_E01_022_Q01.pngwh=80%mx-autosty≤=background:white;><br>Hencegraphbetween-(d[A])/(dt) and time will be:
View Solution