The gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
GMa2
GMa3
GM2a
zero
The correct Answer is:D
To find the gravitational field due to a uniform solid sphere of mass M and radius a at the center of the sphere, we can follow these steps:
1. Understanding the Gravitational Field:
The gravitational field E at a distance r from the center of a sphere is given by the formula:
E=G⋅Mr2
where G is the gravitational constant, M is the mass of the sphere, and r is the distance from the center of the sphere.
2. Identifying the Point of Interest:
In this case, we are interested in the gravitational field at the center of the sphere. Therefore, we need to set r=0 since we are measuring the gravitational field at the center.
3. Applying the Formula:
Substituting r=0 into the formula for the gravitational field:
E=G⋅M02
However, this results in an undefined expression because division by zero is not possible.
4. Understanding the Concept:
According to the shell theorem, the gravitational field inside a uniform solid sphere is zero. This means that at any point inside the sphere, including the center, the gravitational field is zero due to the symmetrical distribution of mass around that point.
5. Conclusion:
Therefore, the gravitational field at the center of the uniform solid sphere is:
E=0
Final Answer:
The gravitational field due to a uniform solid sphere of mass M and radius a at the center of the sphere is 0.
---
The gravitational field E at a distance r from the center of a sphere is given by the formula:
E=G⋅Mr2
where G is the gravitational constant, M is the mass of the sphere, and r is the distance from the center of the sphere.
In this case, we are interested in the gravitational field at the center of the sphere. Therefore, we need to set r=0 since we are measuring the gravitational field at the center.
Substituting r=0 into the formula for the gravitational field:
E=G⋅M02
However, this results in an undefined expression because division by zero is not possible.
According to the shell theorem, the gravitational field inside a uniform solid sphere is zero. This means that at any point inside the sphere, including the center, the gravitational field is zero due to the symmetrical distribution of mass around that point.
Therefore, the gravitational field at the center of the uniform solid sphere is:
E=0
The gravitational field due to a uniform solid sphere of mass M and radius a at the center of the sphere is 0.
Topper's Solved these Questions
Similar Questions
A uniform solid of valume mass density ρ and radius R is shown in figure.
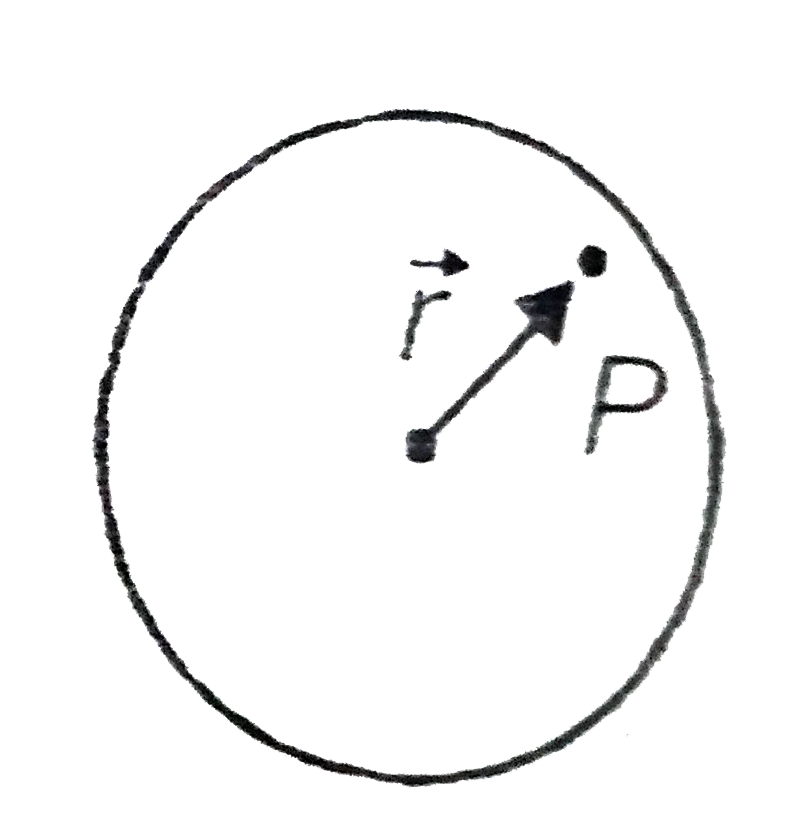
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View Solution
Knowledge Check
Gravitational field due to a solid sphere
Aremains constant throughout the sphereBincrease inside the sphere and decreases outside the sphereCincreases throughout with distance from the centerDdecreases throughout with distance from the centreThe moment of inertia of a solid sphere of mass ‘M' and radius 'R' about a tangent to the sphere is
A25MR2B63MR2C45MR2D75MR2A uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
A8GM2R2B2GM2√3R2C3GM22R2D√32GM2R2
A uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centre of the cavity)
[Here g=(GM)/R2, where M is the mass of the sphere
View Solution
Statement I: The magnitude of the gravitational potential at the surface of solid sphere is less than that of the centre of sphere. Statement II: Due to the solid sphere, the gravitational potential is the same within the sphere.
View Solution
