The gravitational potential energy of an isolated system of three particles, each of mass m, at the three corners of an equilateral triangle of side l is
−Gm2l
−Gm22l
−2Gm2l
−3Gm2l
The correct Answer is:D
To find the gravitational potential energy of an isolated system of three particles, each of mass m, located at the corners of an equilateral triangle with side length l, we can follow these steps:
1. Identify the Masses and Configuration:
- We have three particles, each of mass m, placed at the corners of an equilateral triangle.
- Let's denote the corners of the triangle as A, B, and C.
2. Calculate the Gravitational Potential Energy Between Each Pair of Masses:
- The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by the formula:
U=−Gm1m2r
- In our case, since all masses are equal (m1=m2=m=m3), and the distance between any two masses is l:
UAB=−Gmml=−Gm2l
UBC=−Gmml=−Gm2l
UCA=−Gmml=−Gm2l
3. Sum the Gravitational Potential Energies:
- The total gravitational potential energy Utotal of the system is the sum of the potential energies of all pairs:
Utotal=UAB+UBC+UCA
- Substituting the values we calculated:
Utotal=−Gm2l−Gm2l−Gm2l
Utotal=−3Gm2l
4. Final Result:
- Therefore, the gravitational potential energy of the isolated system of three particles is:
Utotal=−3Gm2l
Conclusion:
The gravitational potential energy of the system is −3Gm2l.
- We have three particles, each of mass m, placed at the corners of an equilateral triangle.
- Let's denote the corners of the triangle as A, B, and C.
- The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by the formula:
U=−Gm1m2r
- In our case, since all masses are equal (m1=m2=m=m3), and the distance between any two masses is l:
UAB=−Gmml=−Gm2l
UBC=−Gmml=−Gm2l
UCA=−Gmml=−Gm2l
- The total gravitational potential energy Utotal of the system is the sum of the potential energies of all pairs:
Utotal=UAB+UBC+UCA
- Substituting the values we calculated:
Utotal=−Gm2l−Gm2l−Gm2l
Utotal=−3Gm2l
- Therefore, the gravitational potential energy of the isolated system of three particles is:
Utotal=−3Gm2l
The gravitational potential energy of the system is −3Gm2l.
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
The gravitational potential energy of a system of three particles of mass m each kept at the vertices of equilateral triangle of side x will be
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionFind the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
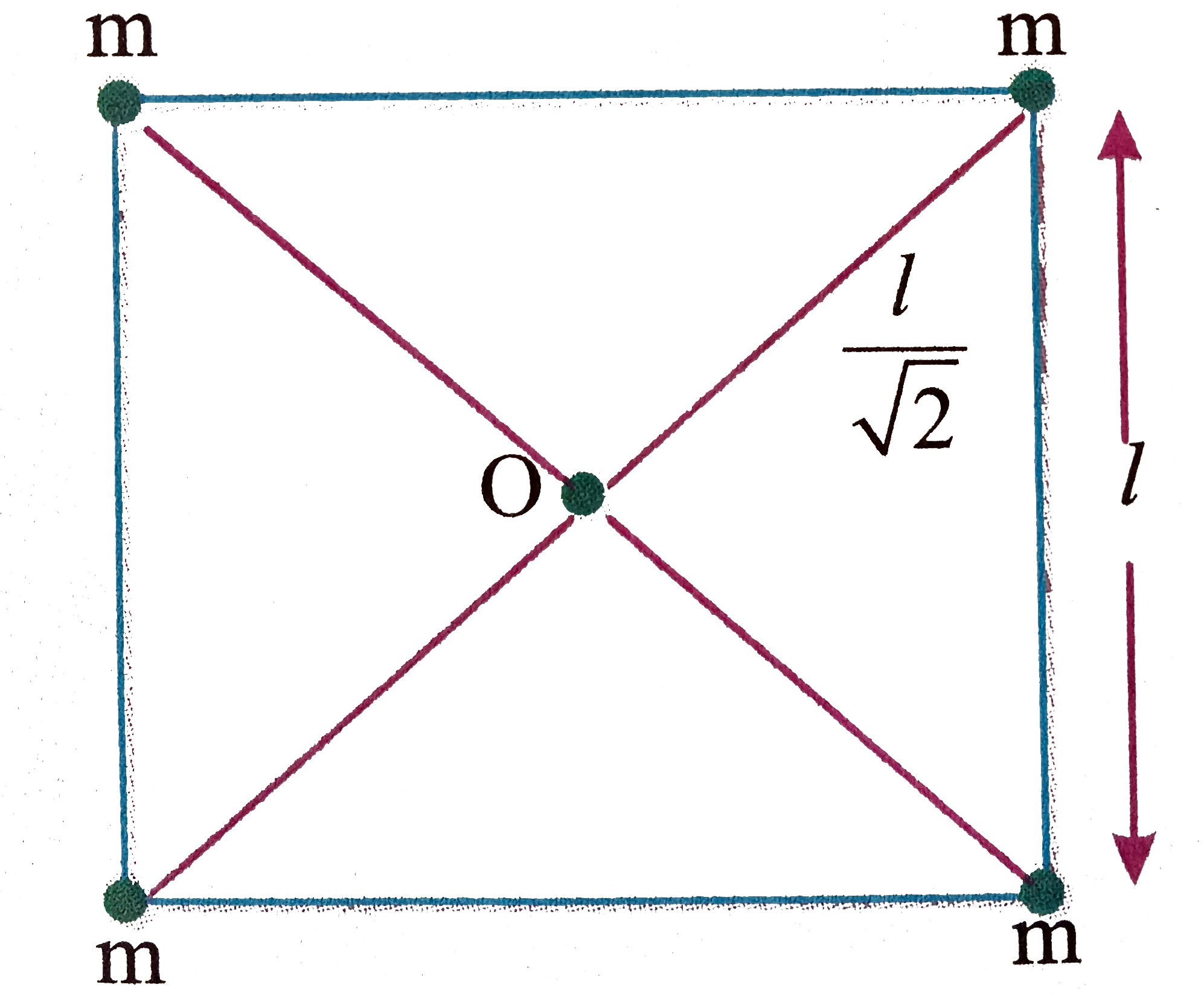
View SolutionLocate the centre of mass of a system of three particles 1.0 kg, 2.0 kg and 3.0 kg placed at the corners of an equilateral traingular of side 1m.
View SolutionFind the potential energy of a system of 3 particles kept at the vertices of an equilateral triangle of side r.
View SolutionThe position co-ordinates of the centre of mass of a system of three particles of equal masses which are placed on the verctices of an equilateral triangle of a side a are shown. Locate centre mass?

View SolutionTwo north poles each of pole strength m and a south pole of pole strength m are placed at the three corners of an equilateral triangle of side a. The intensity of magnetic induction field strength at the centre of the triangle is
View SolutionFind the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
View SolutionThree paricles, each of mass m and carrying a charge q each, are suspended from a common pointby insulating massless strings each of length L. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle. Assume L>>a.
View SolutionThree identical dipoles with charges q and −q, and separation A between the charges, are placed at the corners of an equilateral triangle of side D as shown in (Fig. 3.123). Find the interaction energy of the system (a<<d).
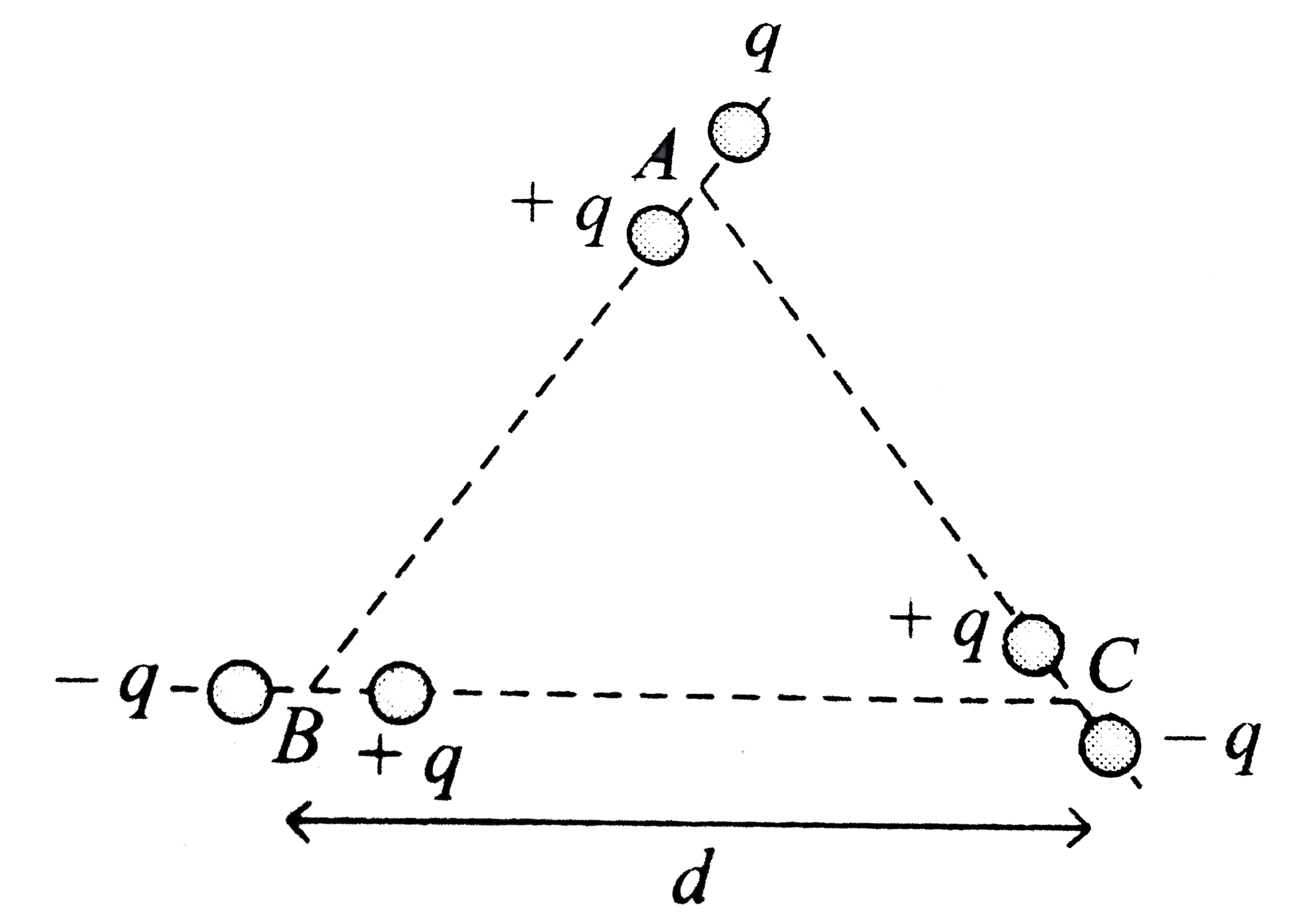 .
.
View Solution
