The heat is flowing through a rod of length 50 cm and area of cross-section 5cm2 . Its ends are respectively at 25∘C and 125∘C . The coefficient of thermal conductivity of the material of the rod is 0.092kcal/m×s×.∘C . The temperature gradient in the rod is
2∘C/cm
2∘C/m
20∘C/m
20∘C/cm
The correct Answer is:A
To find the temperature gradient in the rod, we can follow these steps:
Step 1: Identify the given values
- Length of the rod (L) = 50 cm = 0.5 m (since we will convert to meters for standard units)
- Temperature at one end (T1) = 25°C
- Temperature at the other end (T2) = 125°C
- Change in temperature (ΔT) = T2 - T1 = 125°C - 25°C = 100°C
- Length of the rod in meters (Δx) = 0.5 m
Step 2: Calculate the temperature gradient
The temperature gradient (∇T) is defined as the change in temperature per unit length. It can be calculated using the formula:
Temperature Gradient(∇T)=ΔTΔx
Substituting the values we have:
∇T=100°C0.5m=200°C/m
Step 3: Convert the temperature gradient to cm
Since the original length was given in centimeters, we can convert the temperature gradient to °C/cm:
∇T=200°C/m=20°C/10cm=20°C/cm
Final Answer
So, the temperature gradient in the rod is:
∇T=200°C/m or 20°C/cm
---
- Length of the rod (L) = 50 cm = 0.5 m (since we will convert to meters for standard units)
- Temperature at one end (T1) = 25°C
- Temperature at the other end (T2) = 125°C
- Change in temperature (ΔT) = T2 - T1 = 125°C - 25°C = 100°C
- Length of the rod in meters (Δx) = 0.5 m
The temperature gradient (∇T) is defined as the change in temperature per unit length. It can be calculated using the formula:
Since the original length was given in centimeters, we can convert the temperature gradient to °C/cm:
So, the temperature gradient in the rod is:
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Convection
13 Videos
- TRANSMISSION OF HEATBOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Radiation (General, Kirchoff s law, Black body)
38 Videos
- THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY BOOK - ERRORLESS CHAPTER - THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY EXERCISE - Self Evaluation Test
15 Videos
- UNITS, DIMENSION & MEASUREMENTSBOOK - ERRORLESS CHAPTER - UNITS, DIMENSION & MEASUREMENTSEXERCISE - All Questions
333 Videos
Similar Questions
Heat is flowing through a rod of length 25.0cm having cross-sectional area 8.80cm2. The coefficient of thermal conductivity for the material of the rod is K=9.2×10−2kcals−1m−1.∘C−1. The Temperatures of the ends of the rod are 125∘C and 0∘C in the steady state. Calculate (i) temeprature gradient in the rod (ii) temperature of a point at a distance of 10.0cm from the hot end and (iii) rate of flow of heat.
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View Solution
Knowledge Check
A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLThe ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK
 AThe temperature of rod at centre is 250∘CBThe temperature of rod at centre is 50∘CCThe temperature gradient in right half is 500∘C/mDThe temperature gradient in left half is 300∘C/m
AThe temperature of rod at centre is 250∘CBThe temperature of rod at centre is 50∘CCThe temperature gradient in right half is 500∘C/mDThe temperature gradient in left half is 300∘C/mA cylindrical rod of aluminium is of length 20 cm and radius 2 cm. The two ends are maintained at temperatures of 0∘C and 50∘C the coefficient of thermal conductivity is 0.5 calcm×sec×∘C. Then the thermal resistance of the rod in calsec×∘C is
A318B31.8C3.18D0.318
Find the thermal resistance of an aluminium rod of length 20cm and area of cross section 1cm2 . The heat current is along the length of the rod. Thermal conductivity of aluminium =200Wm−1K−1 .
View SolutionIn the following situations, the length and area of cross-section of each rod is same. Find temperature θ at junction of rods.
(a)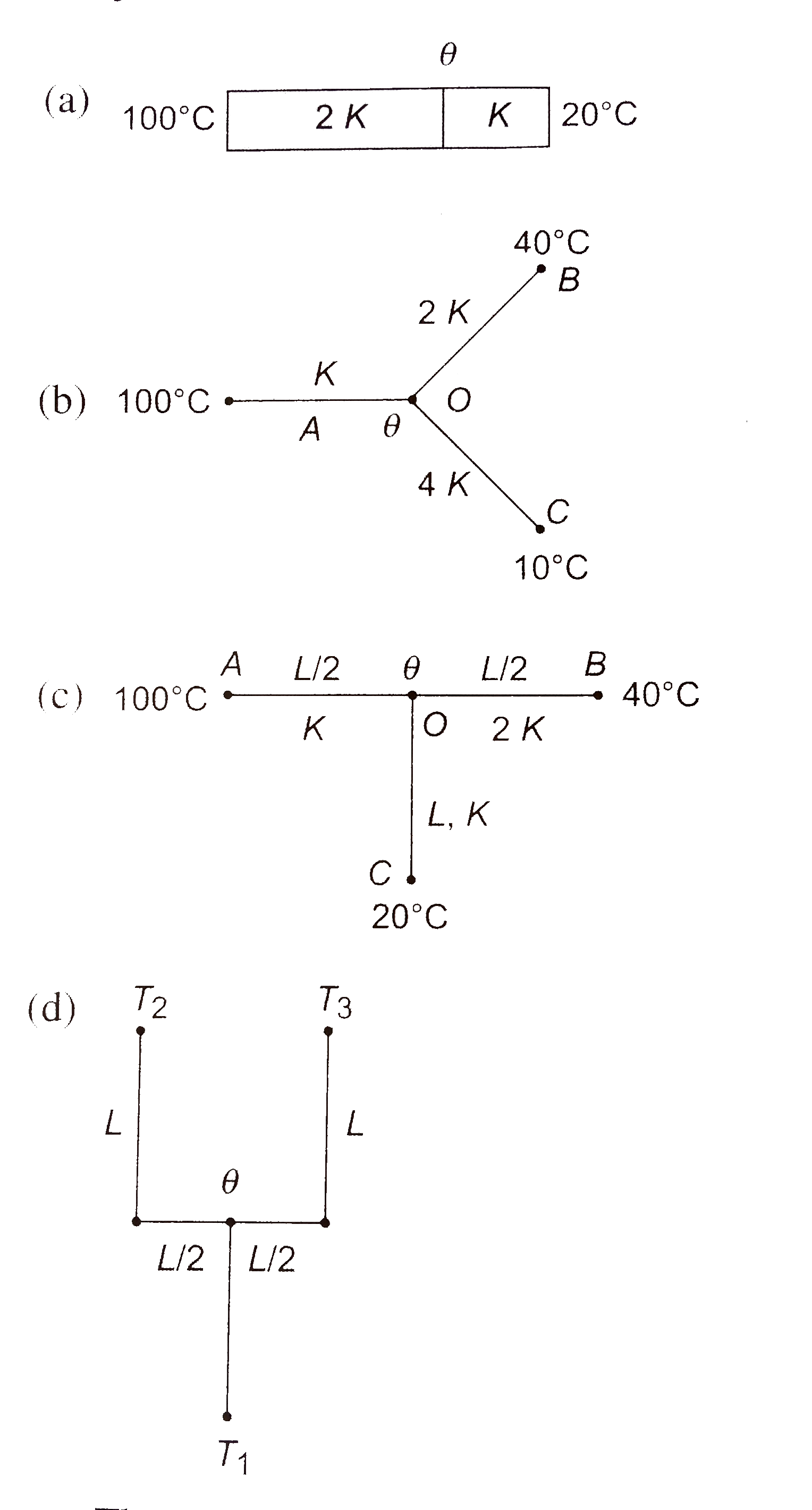
(b)
(c )
(d)
The thermal conductivity of each rod is K.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionA rod of 1m length and area of cross-section 1cm2 is connected across two heat reservoirs at temperature 100∘C and 0∘C as shown. The heat flow per second through the rod in steady state will be [Thermal conductivity of material of rod =0.09kilocalm−1s−1('∘C)]

View SolutionTwo rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
View Solution
