The kinetic energy K of a particle moving along a circle of radius R depends on the distance covered s as K=as2. The force acting on the particle is
The correct Answer is:2as2r
mv2/2=as2,mv2=2as2,F2=mv2/r=2as2/R
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (FROM BANKING OR RAILS AND ROADS)
13 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS)
14 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (FROM ANGULAR VELOCITY)
4 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
The kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View SolutionThe kinetic energy of a particle moving along a circle of radius R depends on the distance covered s as K.E = KS2 where K is a constant. Find the force acting on the particle as a function of S -
View SolutionThe kinetic energy of a particle moving along a circle of radius R depends on the distance covered S as K =α.S2, where α is a constant. Find the force acting on the particle as a function of S.
View Solution(a) A ball, suspended by a thread, swings in a vertical plane so that its acceleration in the extreme and the lowest positions are equal. The angle θ of thread deflection in the extreme position will be
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the force acting on the particle as a function of s.
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance S as K=βS2 , where β is a constant. Tangential acceleration of the particle is proportional to
View SolutionThe kinetic energy K of a particle moving along x - axis varies with its position (x) as shown in figure
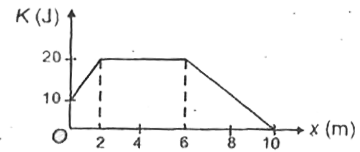
The magnitude of force acting on particle at x = 9 mis
View SolutionKinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
View SolutionKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View Solution
