(a) A ball, suspended by a thread, swings in a vertical plane so that its acceleration in the extreme and the lowest positions are equal. The angle of thread deflection in the extreme position will be
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as , where 'a' is a constant. Find the force acting on the particle as a function of s.
The correct Answer is:(a) , ( b)
Step-by-Step Solution
1. Understanding the Problem:
- A ball is suspended by a thread and swings in a vertical plane. The acceleration at the extreme position and the lowest position is equal. We need to find the angle θ of the thread deflection in the extreme position.
2. Acceleration at the Extreme Position:
- At the extreme position, the tangential acceleration at is given by:
at=gsinθ
- At the lowest position, the centripetal acceleration ac is given by:
ac=v2L
- Since the acceleration in both positions is equal, we can set them equal to each other:
gsinθ=v2L
3. Using Energy Conservation:
- The potential energy at the extreme position is converted into kinetic energy at the lowest position. The height h can be expressed as:
h=L−Lcosθ=L(1−cosθ)
- The potential energy at the extreme position is:
PE=mgh=mgL(1−cosθ)
- The kinetic energy at the lowest position is:
KE=12mv2
- By conservation of energy:
mgL(1−cosθ)=12mv2
- Canceling m from both sides gives:
gL(1−cosθ)=12v2
4. Substituting for v2:
- From the earlier equation gsinθ=v2L, we can express v2 as:
v2=gLsinθ
- Substituting this into the energy equation gives:
gL(1−cosθ)=12gLsinθ
5. Simplifying the Equation:
- Dividing both sides by gL (assuming gL≠0):
1−cosθ=12sinθ
- Rearranging gives:
2(1−cosθ)=sinθ
6. Using Trigonometric Identities:
- We can use the identity sin2θ+cos2θ=1 to express sinθ in terms of cosθ:
2−2cosθ=√1−cos2θ
- Squaring both sides and simplifying will lead to the final expression for θ.
7. Final Result:
- After solving the trigonometric equation, we find:
θ=2tan−1(1/2)
Part (b)
1. Understanding the Problem:
- The kinetic energy T of a particle moving in a circle of radius R depends on the distance s covered as T=as2, where a is a constant. We need to find the force acting on the particle as a function of s.
2. Relating Kinetic Energy to Velocity:
- The kinetic energy is given by:
T=12mv2
- Setting this equal to the given expression:
12mv2=as2
- Rearranging gives:
mv2=2as2
3. Finding Velocity:
- From the above equation, we can express v2:
v2=2as2m
4. Finding the Centripetal Force:
- The centripetal force Fc required to keep the particle moving in a circle is given by:
Fc=mv2R
- Substituting v2:
Fc=m(2as2/m)R=2as2R
5. Finding the Total Force:
- The total force acting on the particle is the sum of the centripetal force and any tangential force. Since we are only considering the centripetal force in this case, we have:
F=2as2R
6. Final Result:
- The force acting on the particle as a function of s is:
F(s)=2as2R
- A ball is suspended by a thread and swings in a vertical plane. The acceleration at the extreme position and the lowest position is equal. We need to find the angle θ of the thread deflection in the extreme position.
- At the extreme position, the tangential acceleration at is given by:
at=gsinθ
- At the lowest position, the centripetal acceleration ac is given by:
ac=v2L
- Since the acceleration in both positions is equal, we can set them equal to each other:
gsinθ=v2L
- The potential energy at the extreme position is converted into kinetic energy at the lowest position. The height h can be expressed as:
h=L−Lcosθ=L(1−cosθ)
- The potential energy at the extreme position is:
PE=mgh=mgL(1−cosθ)
- The kinetic energy at the lowest position is:
KE=12mv2
- By conservation of energy:
mgL(1−cosθ)=12mv2
- Canceling m from both sides gives:
gL(1−cosθ)=12v2
- From the earlier equation gsinθ=v2L, we can express v2 as:
v2=gLsinθ
- Substituting this into the energy equation gives:
gL(1−cosθ)=12gLsinθ
- Dividing both sides by gL (assuming gL≠0):
1−cosθ=12sinθ
- Rearranging gives:
2(1−cosθ)=sinθ
- We can use the identity sin2θ+cos2θ=1 to express sinθ in terms of cosθ:
2−2cosθ=√1−cos2θ
- Squaring both sides and simplifying will lead to the final expression for θ.
- After solving the trigonometric equation, we find:
θ=2tan−1(1/2)
- The kinetic energy T of a particle moving in a circle of radius R depends on the distance s covered as T=as2, where a is a constant. We need to find the force acting on the particle as a function of s.
- The kinetic energy is given by:
T=12mv2
- Setting this equal to the given expression:
12mv2=as2
- Rearranging gives:
mv2=2as2
- From the above equation, we can express v2:
v2=2as2m
- The centripetal force Fc required to keep the particle moving in a circle is given by:
Fc=mv2R
- Substituting v2:
Fc=m(2as2/m)R=2as2R
- The total force acting on the particle is the sum of the centripetal force and any tangential force. Since we are only considering the centripetal force in this case, we have:
F=2as2R
- The force acting on the particle as a function of s is:
F(s)=2as2R
Similar Questions
(a) A ball, suspended by a thread, swings in a vertical plane so that its acceleration in the extreme and the lowest positions are equal. The angle θ of thread deflection in the extreme position will be
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the force acting on the particle as a function of s.
View SolutionThe kinetic energy of a particle moving along a circle of radius R depends on the distance covered S as K =α.S2, where α is a constant. Find the force acting on the particle as a function of S.
View Solution
Knowledge Check
In simple harmonic motion, at the extreme positions
Akinetic energy is minimum, potential energy is maximumBkinetic energy is maximum, potential energy is minimumCboth kinetic and potential energies are maximum.Dboth kinetic and potential energies are minimum
The kinetic energy of a particle moving along a circle of radius R depends on the distance covered s as K.E = KS2 where K is a constant. Find the force acting on the particle as a function of S -
View SolutionA ball suspended by a thread swing in a vertical plane that its acceleration values in the lowest possition and the extreme postition are equal . Find the thread deffection angle in the extreme possition.
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance S as K=βS2 , where β is a constant. Tangential acceleration of the particle is proportional to
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View SolutionThe speed of a particle moving in a circle of radius r=2m varies with time t as v=t2, where t is in second and v in m/s. Find the radial, tangential and net acceleration at t=2s.
View SolutionA ball attached to one end of a string swings in a vertical plane such that its acceleration at point A (extreme position) is equal to its acceleration at point B (mean position), The angle θ is
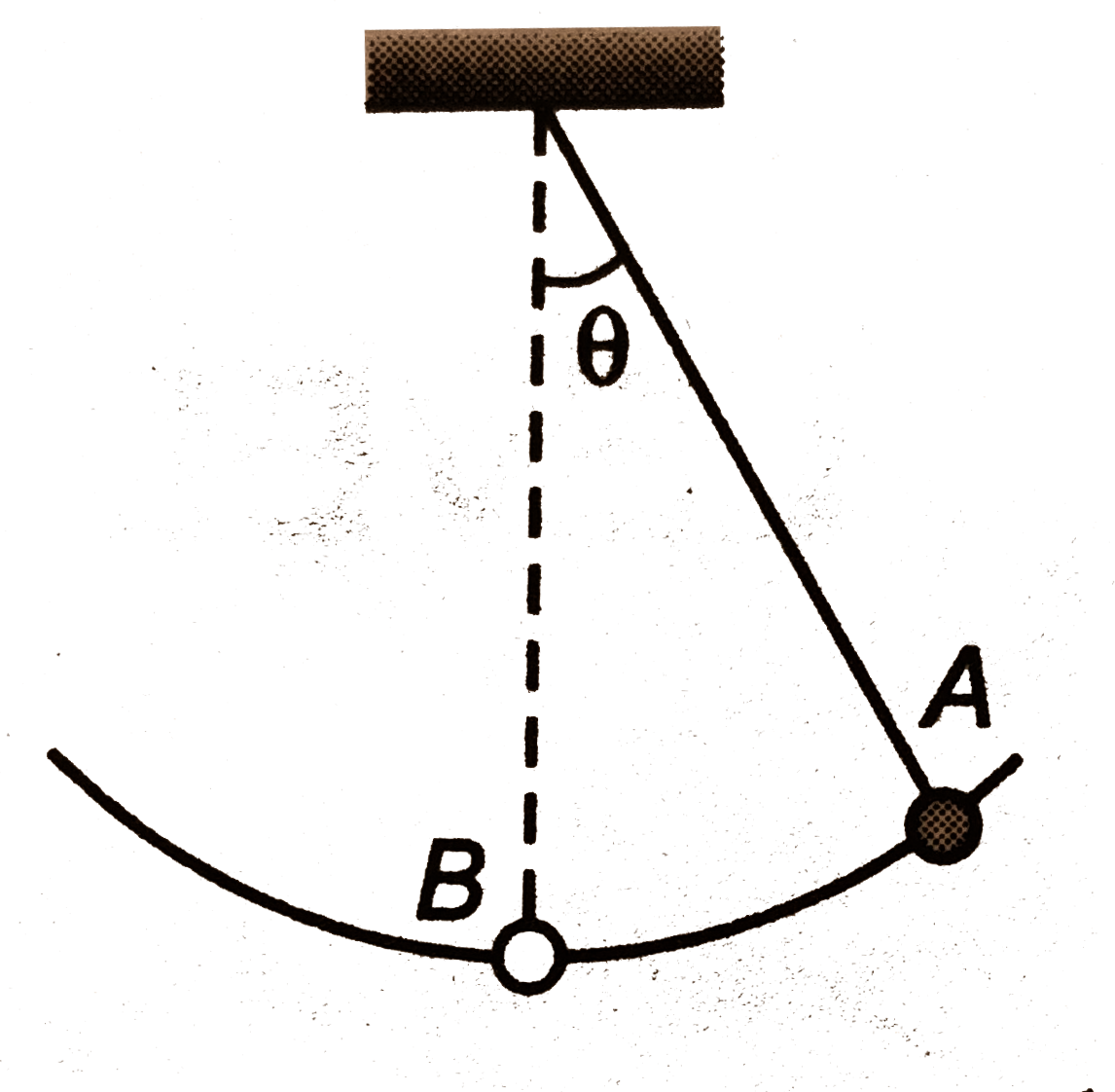
View SolutionA rod of mass m and length l suspended from a point swings in a vertica plane such that magnitude of acceleration of its C.M. at extreme points is same as that at the mean point then :
View Solution
