The length of a potentiometer wire is 600 cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be at 500cm. On connecting a voltmeter acros the cell, the balancing length is decreased by 10cm
The resistance of the voltmeter is
500Ω
290Ω
490Ω
20Ω
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the given data
- Length of the potentiometer wire (L) = 600 cm
- Current (I) = 40 mA = 0.04 A
- EMF of the cell (E) = 2 V
- Internal resistance of the cell (r) = 10 Ω
- Initial balancing length (L1) = 500 cm
- New balancing length after connecting the voltmeter (L2) = 490 cm
Step 2: Calculate the potential drop per unit length of the potentiometer wire
The potential drop across the potentiometer wire can be calculated using the formula:
V=E−I⋅r
Substituting the values:
V=2V−(0.04A⋅10Ω)
V=2V−0.4V=1.6V
Now, the potential drop per unit length (V) can be calculated as:
V=Total potential dropLength of the wire=1.6V600cm=1.6V6m=1.6V600cm
Step 3: Calculate the potential drop across the wire at the initial balancing length
Using the initial balancing length (L1 = 500 cm):
V1=1.6V600cm⋅500cm=1.6⋅500600=800600=43V
Step 4: Calculate the potential drop across the wire at the new balancing length
Using the new balancing length (L2 = 490 cm):
V2=1.6V600cm⋅490cm=1.6⋅490600=784600=392300V
Step 5: Set up the equation for the voltmeter
When the voltmeter is connected, the potential drop across it can be expressed as:
V2=E−I⋅(r+RV)
Where RV is the resistance of the voltmeter.
Step 6: Substitute and solve for RV
From the previous steps, we have:
1. V2=392/300V
2. E=2V
3. I=Er+RV
Substituting the values:
392300=2−210+RV
Step 7: Cross-multiply and solve for RV
Cross-multiplying gives:
392(10+RV)=600(2−210+RV)
Solving this equation will yield the resistance of the voltmeter RV.
Final Calculation:
After simplifying the equation, we find:
RV=490Ω
Conclusion:
The resistance of the voltmeter is 490Ω.
---
- Length of the potentiometer wire (L) = 600 cm
- Current (I) = 40 mA = 0.04 A
- EMF of the cell (E) = 2 V
- Internal resistance of the cell (r) = 10 Ω
- Initial balancing length (L1) = 500 cm
- New balancing length after connecting the voltmeter (L2) = 490 cm
The potential drop across the potentiometer wire can be calculated using the formula:
V=E−I⋅r
Substituting the values:
V=2V−(0.04A⋅10Ω)
V=2V−0.4V=1.6V
V=Total potential dropLength of the wire=1.6V600cm=1.6V6m=1.6V600cm
Using the initial balancing length (L1 = 500 cm):
V1=1.6V600cm⋅500cm=1.6⋅500600=800600=43V
Using the new balancing length (L2 = 490 cm):
V2=1.6V600cm⋅490cm=1.6⋅490600=784600=392300V
When the voltmeter is connected, the potential drop across it can be expressed as:
V2=E−I⋅(r+RV)
Where RV is the resistance of the voltmeter.
From the previous steps, we have:
1. V2=392/300V
2. E=2V
3. I=Er+RV
392300=2−210+RV
Cross-multiplying gives:
392(10+RV)=600(2−210+RV)
After simplifying the equation, we find:
RV=490Ω
The resistance of the voltmeter is 490Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Subjective
13 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example
65 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 More Than One Correct
10 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
The length of a potentiometer wire is 600cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be ast 500cm. On connecting a voltmeter acros the cell, the balancing length is decreased by 10cm
The voltmeter reading will be
View SolutionThe length of a potentiometer wire AB is 600cm, and it carries a constant current of 40mA from A to B. For a cell of emf 2V and internal resistance 10Ω, the null point is found at 500cm from A. When a voltmeter is connected across the cell, the balancing length of the wire is decreased by 10cm.
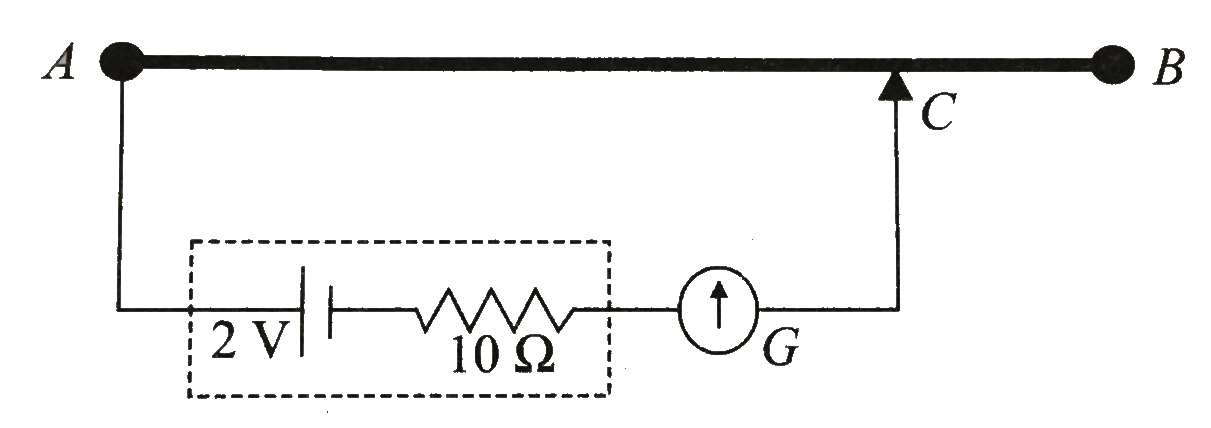
Potential gradient along AB is
View SolutionThe potentiometer wire is of length 1200 cam and it carries a current of 60 mA. For a cell of emf 5V and internal resistance of 20Ω, the null point of it is found to be at 1000 cm.The resistance of potentiometer wire is
View SolutionThe length of the potentiometer wire is 600 cm and a current of 40 mA is flowing in it. When a cell of emf 2 V and internal resistance 10Ω is balanced on this potentiometer the balance length is found to be 500 cm. The resistance of potentiometer wire will be
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of e.m.f. 2V and internal resistance 1Ω. The current flowing through the potentiometer wire is
View SolutionThere is a potentiometer wire of length 1200 cm and 60 mA current is flowing in it. A battery of emf 5V and internal resistance of 20ohm is balanced on potentiometer wire with balancing length 1000 cm. The resistance of potentiometer wire is
View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View SolutionIn a potentiometer experiment the balancing with a cell is at length 240 cm. On shunting the cell with a resistance of 2Ω, the balancing length becomes 120 cm.The internal resistance of the cell is
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of emf 2 volt and internal resistance 1Ω. If a cell of emf 1.2 volt is balanced by it, the balancing length will be
View SolutionA voltmeter of resistance 998Ω is connected across a cell of emf 2 V and internal resistance 2Ω. Find the p.d. across the voltmeter, that across the terminals of the cell and percentage error in the reading of the voltmeter.
View Solution
