The length of a potentiometer wire is 600 cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be at 500cm. On connecting a voltmeter acros the cell, the balancing length is decreased by 10cm
The resistance of the voltmeter is
400Ω
500Ω
510Ω
490Ω
The correct Answer is:D
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the given data
- Length of the potentiometer wire (L) = 600 cm
- Current (I) = 40 mA = 0.04 A
- EMF of the cell (E) = 2 V
- Internal resistance of the cell (r) = 10 Ω
- Initial balancing length (l1) = 500 cm
- New balancing length after connecting the voltmeter (l2) = 490 cm
Step 2: Calculate the resistance per cm of the potentiometer wire
The resistance of the potentiometer wire can be calculated using the formula:
Rwire=rtotalL
Where rtotal is the resistance corresponding to the initial balancing length.
The total resistance for the initial balancing length (500 cm) can be calculated as:
rtotal=rl1
rtotal=10Ω500cm=150Ω/cm
Step 3: Calculate the total resistance for the new balancing length
Now, we calculate the resistance corresponding to the new balancing length (490 cm):
rnew=150×490=49050=9.8Ω
Step 4: Set up the equation for the equivalent resistance
When the voltmeter is connected across the cell, the equivalent resistance Req of the voltmeter Rv and the internal resistance r of the cell is in parallel:
Req=Rv⋅rRv+r
This equivalent resistance should equal the resistance corresponding to the new balancing length:
Req=9.8Ω
Step 5: Substitute and solve for Rv
Substituting the values into the equation:
Rv⋅10Rv+10=9.8
Cross-multiplying gives:
Rv⋅10=9.8(Rv+10)
10Rv=9.8Rv+98
Rearranging the equation:
10Rv−9.8Rv=98
0.2Rv=98
Now, solving for Rv:
Rv=980.2=490Ω
Final Answer
The resistance of the voltmeter is Rv=490Ω.
---
- Length of the potentiometer wire (L) = 600 cm
- Current (I) = 40 mA = 0.04 A
- EMF of the cell (E) = 2 V
- Internal resistance of the cell (r) = 10 Ω
- Initial balancing length (l1) = 500 cm
- New balancing length after connecting the voltmeter (l2) = 490 cm
The resistance of the potentiometer wire can be calculated using the formula:
Rwire=rtotalL
Where rtotal is the resistance corresponding to the initial balancing length.
rtotal=rl1
rtotal=10Ω500cm=150Ω/cm
Now, we calculate the resistance corresponding to the new balancing length (490 cm):
rnew=150×490=49050=9.8Ω
When the voltmeter is connected across the cell, the equivalent resistance Req of the voltmeter Rv and the internal resistance r of the cell is in parallel:
Req=Rv⋅rRv+r
Req=9.8Ω
Substituting the values into the equation:
Rv⋅10Rv+10=9.8
Rv⋅10=9.8(Rv+10)
10Rv=9.8Rv+98
10Rv−9.8Rv=98
0.2Rv=98
Rv=980.2=490Ω
The resistance of the voltmeter is Rv=490Ω.
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Integer
8 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Assertion-Reasoning
7 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type
7 Videos
Similar Questions
The length of a potentiometer wire is 600cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be ast 500cm. On connecting a voltmeter acros the cell, the balancing length is decreased by 10cm
The voltmeter reading will be
View SolutionThe length of a potentiometer wire AB is 600cm, and it carries a constant current of 40mA from A to B. For a cell of emf 2V and internal resistance 10Ω, the null point is found at 500cm from A. When a voltmeter is connected across the cell, the balancing length of the wire is decreased by 10cm.
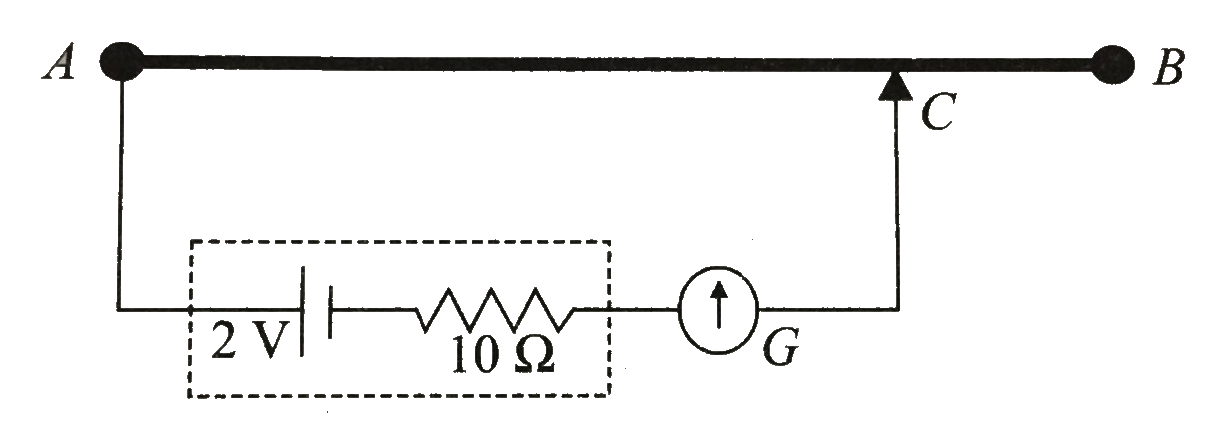
Potential gradient along AB is
View SolutionThe potentiometer wire is of length 1200 cam and it carries a current of 60 mA. For a cell of emf 5V and internal resistance of 20Ω, the null point of it is found to be at 1000 cm.The resistance of potentiometer wire is
View SolutionThe length of the potentiometer wire is 600 cm and a current of 40 mA is flowing in it. When a cell of emf 2 V and internal resistance 10Ω is balanced on this potentiometer the balance length is found to be 500 cm. The resistance of potentiometer wire will be
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of e.m.f. 2V and internal resistance 1Ω. The current flowing through the potentiometer wire is
View SolutionThere is a potentiometer wire of length 1200 cm and 60 mA current is flowing in it. A battery of emf 5V and internal resistance of 20ohm is balanced on potentiometer wire with balancing length 1000 cm. The resistance of potentiometer wire is
View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View SolutionIn a potentiometer experiment the balancing with a cell is at length 240 cm. On shunting the cell with a resistance of 2Ω, the balancing length becomes 120 cm.The internal resistance of the cell is
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of emf 2 volt and internal resistance 1Ω. If a cell of emf 1.2 volt is balanced by it, the balancing length will be
View SolutionA voltmeter of resistance 998Ω is connected across a cell of emf 2 V and internal resistance 2Ω. Find the p.d. across the voltmeter, that across the terminals of the cell and percentage error in the reading of the voltmeter.
View Solution
