The magnetic field inn a region is given by →B=→kB0LywhereLisafixed≤n>h.Aconduct∈grodof≤n>hLliesalongtheY−aξsbetweentheorig∈andthep∮(0,L,0).Iftherodmoveswithavelocityv= v_0 veci, find the emf induced between the ends of the rod.
To find the induced electromotive force (emf) between the ends of a conducting rod moving in a magnetic field, we can follow these steps:
1. Understand the Setup:
- We have a magnetic field given by →B=B0L^ky.
- A conducting rod of length L lies along the Y-axis, from the origin (0,0,0) to the point (0,L,0).
- The rod moves with a velocity →v=v0^i (along the X-axis).
2. Identify the Magnetic Field:
- The magnetic field varies with y as →B depends on y. Thus, at any point y, the magnetic field can be expressed as:
B(y)=B0Ly^k
3. Calculate the Induced emf:
- The induced emf dϵ across a small segment of the rod of length dy can be calculated using the formula:
dϵ=B⋅v⋅dy
- Here, v is the velocity of the rod. Since the rod is moving in the x-direction, we can substitute v=v0.
4. Substituting Values:
- Substitute B(y) and v into the equation:
dϵ=(B0Ly)v0dy
- This gives:
dϵ=B0v0Lydy
5. Integrate to Find Total emf:
- To find the total emf ϵ across the entire length of the rod, integrate dϵ from y=0 to y=L:
ϵ=∫L0B0v0Lydy
- This integral evaluates to:
ϵ=B0v0L(y22)L0=B0v0L⋅L22
6. Simplifying the Result:
- Simplifying the expression gives:
ϵ=B0v0L2
7. Final Answer:
- The induced emf between the ends of the rod is:
ϵ=B0v0L2^k
- We have a magnetic field given by →B=B0L^ky.
- A conducting rod of length L lies along the Y-axis, from the origin (0,0,0) to the point (0,L,0).
- The rod moves with a velocity →v=v0^i (along the X-axis).
- The magnetic field varies with y as →B depends on y. Thus, at any point y, the magnetic field can be expressed as:
B(y)=B0Ly^k
- The induced emf dϵ across a small segment of the rod of length dy can be calculated using the formula:
dϵ=B⋅v⋅dy
- Here, v is the velocity of the rod. Since the rod is moving in the x-direction, we can substitute v=v0.
- Substitute B(y) and v into the equation:
dϵ=(B0Ly)v0dy
- This gives:
dϵ=B0v0Lydy
- To find the total emf ϵ across the entire length of the rod, integrate dϵ from y=0 to y=L:
ϵ=∫L0B0v0Lydy
- This integral evaluates to:
ϵ=B0v0L(y22)L0=B0v0L⋅L22
- Simplifying the expression gives:
ϵ=B0v0L2
- The induced emf between the ends of the rod is:
ϵ=B0v0L2^k
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
Similar Questions
The magnetic field in a region is given by →B=B0Lxˆk where L is a fixed length.A conducting rod of length lies along the X-axis between the origin and the point (L,0,0).If the rod moves with a velocity →v=v0ˆj the emf induced between the ends of the rod.
View SolutionThere is a conducting rod of length 2L that lies along x-axis from x=−L→x=L. If rod moves with velocityv=v0ˆi in the magnetic field→B=B0ˆk, then induced EMF between ends of rod is
View Solution
Knowledge Check
- Question 1 - Select One
A metal rod of length I is moved with velocity v in a uniform magnetic field →B. Emf is induced between the two ends of rod
Awhen →l is parallel to →BBwhen →l is parallel to →vCwhen →v is parallel to →BDnone of the above cases - Question 2 - Select One
The magnetic field in a region is given by →B=B0(1+xa)ˆk. A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity →V=V0ˆi. The emf induced in the loop is
Av0B0d2aBv0B0d3aCv0B0d22aD0
A rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.
 View Solution
View SolutionA wire of length 2l is bent at mid point so that the angle between two halves is 60∘. If it moves as shown with a velocity v in a magnetic field B find the induced emf.
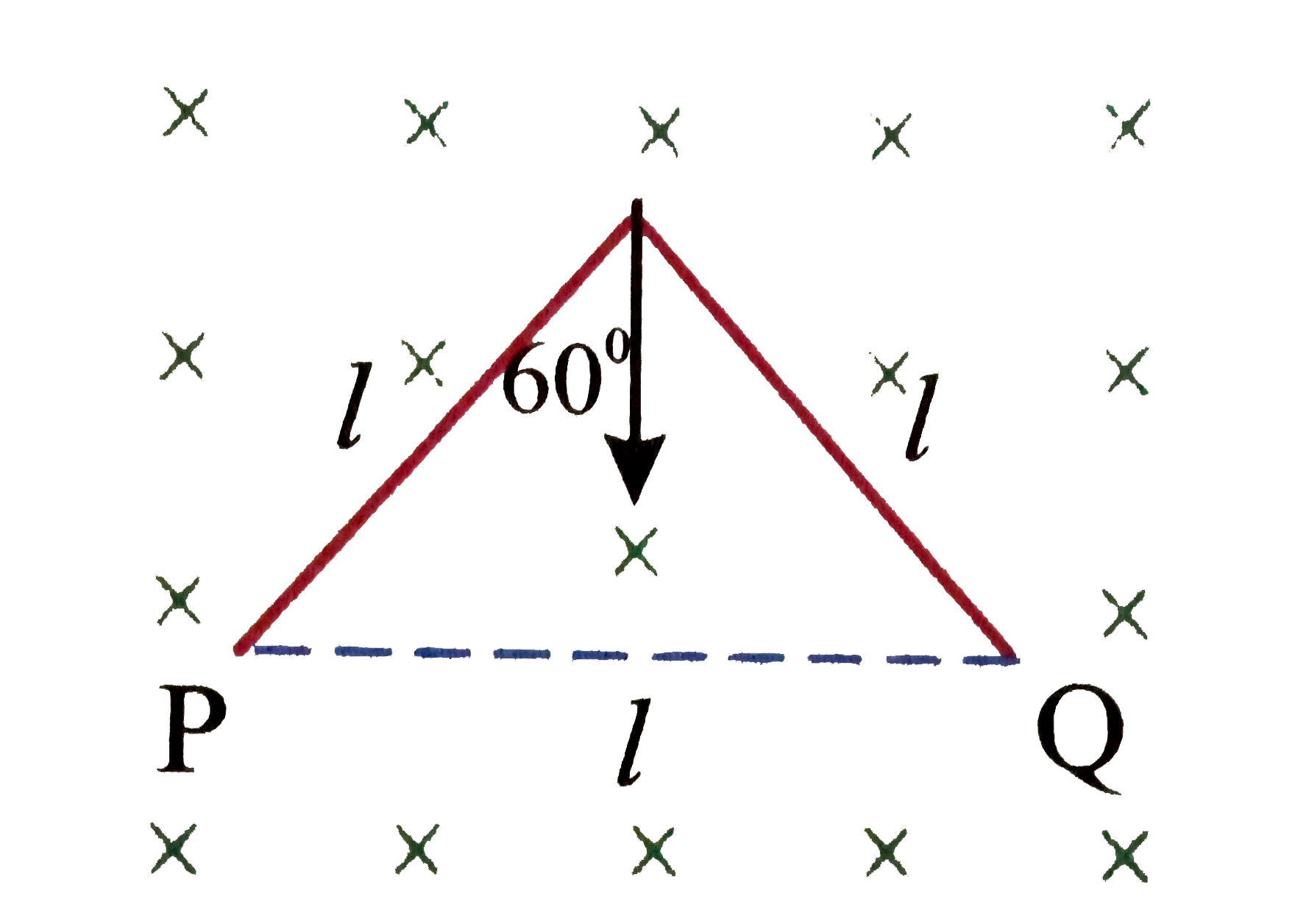 View Solution
View SolutionA conducting rod of length l is kept parallel to a uniform magnetic field →B. It is moved along the magnetic field with a velocity →v. What is the value of emf induced in the conductor?
View SolutionThe magnetic field in a region is given by B=B0(1−XL)K. A straight conductor AB of length 2L, placed with its ends at points A (a,0,0) and B(a,2L,0), carries a current I from A to B. Find the magnetic force on the conductor
View SolutionA glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?
 View Solution
View Solution

