The maximum range of a gun on horizontal terrain is 1km. If g=10ms−2, what must be the muzzle velocity of the shell ?
400ms−1
200ms−1
100ms−1
50ms−1
The correct Answer is:C
To find the muzzle velocity of the shell given the maximum range of a gun on horizontal terrain, we can use the formula for the range of a projectile. The maximum range R is given by the equation:
R=u20sin(2θ)g
Where:
- R is the range,
- u0 is the muzzle velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity.
Step 1: Identify the maximum range and gravitational acceleration
From the problem, we know:
- The maximum range R=1 km=1000 m
- The gravitational acceleration g=10 m/s2
Step 2: Determine the angle for maximum range
The maximum range occurs when the angle of projection θ is 45∘. At this angle, sin(2θ)=sin(90∘)=1.
Step 3: Substitute values into the range formula
Using the maximum range formula, we can rewrite it as:
R=u20g
Substituting the known values:
1000=u2010
Step 4: Solve for u20
To isolate u20, multiply both sides by g:
u20=1000×10
u20=10000
Step 5: Calculate u0
Now, take the square root of both sides to find u0:
u0=√10000
u0=100 m/s
Conclusion
The muzzle velocity of the shell must be 100 m/s.
---
- R is the range,
- u0 is the muzzle velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity.
From the problem, we know:
- The maximum range R=1 km=1000 m
- The gravitational acceleration g=10 m/s2
The maximum range occurs when the angle of projection θ is 45∘. At this angle, sin(2θ)=sin(90∘)=1.
Using the maximum range formula, we can rewrite it as:
To isolate u20, multiply both sides by g:
u20=10000
Now, take the square root of both sides to find u0:
u0=100 m/s
The muzzle velocity of the shell must be 100 m/s.
Topper's Solved these Questions
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - B. Medical entrance
1 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrance
12 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - A. Taking it together
1 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
Similar Questions
The maximum range of a gun from horizontal terrain is 16km. If g=10m/s2 what must be the muzzle velocity of the shell?
View SolutionThe maximum range of a rifle bullet on the horizontal ground is 6km. Find its maximum range on an inclined of 30∘.
View SolutionA gun is mounted on a stationary rail road car. The mass of the car, the gun, the shells and the operator is 50 m, where m is the mass of one shell. Two shells are fired one after the other along same horizontal line in same direction. If the muzzle velocity of the shells is 200 m/s, then find the speed of the car after second shot.
View SolutionA loaded spring gun, initially at rest on a horizontal frictionless surface, fires a marble at angle of elevation theta. The mass of the gun is M, the mass of the marble is m, and the muzzle velocity of the marble is v0. What is the final motion of the gun ?
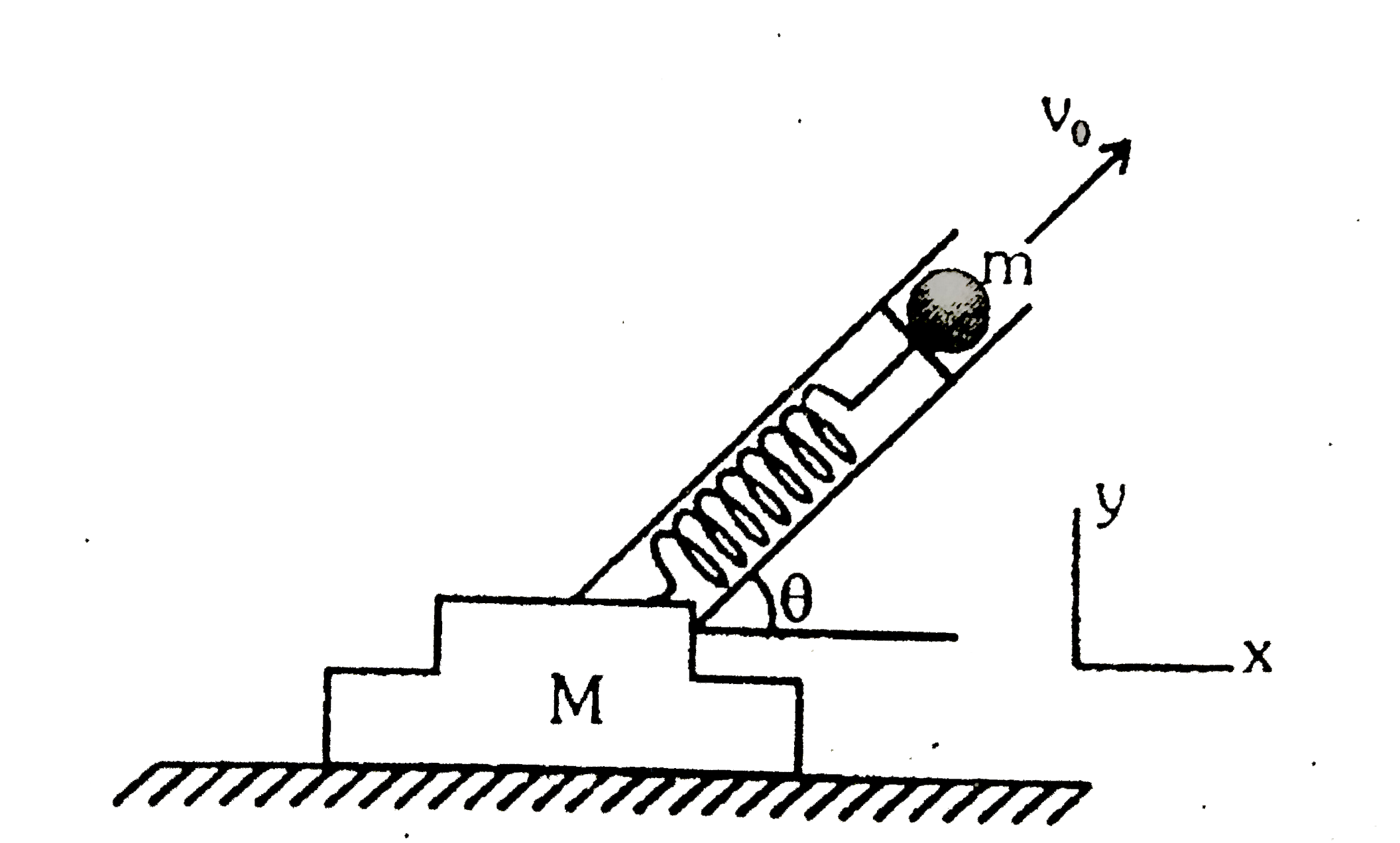
View SolutionSpring Gun Recoil
A loaded spring gun, initially at rest on a horizontal frictionless surface, fires a marble at angle of elevation theta. The mass of the gun is M, the mass of the marble is m, and the muzzle velocity of the marble is v0. What is the final motion of the gun ?

View SolutionA body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5s ? (g=10ms−2).
View SolutionA shell is fired from a long - range gun with an intial velocity u=1000ms−1 at an angle 30∘ to the horizontal. How long with the shell be in the air ? At what distance from the gun will it fall to ground ? The gun and the point where the shell lands are on the same horizontal line .
View Solution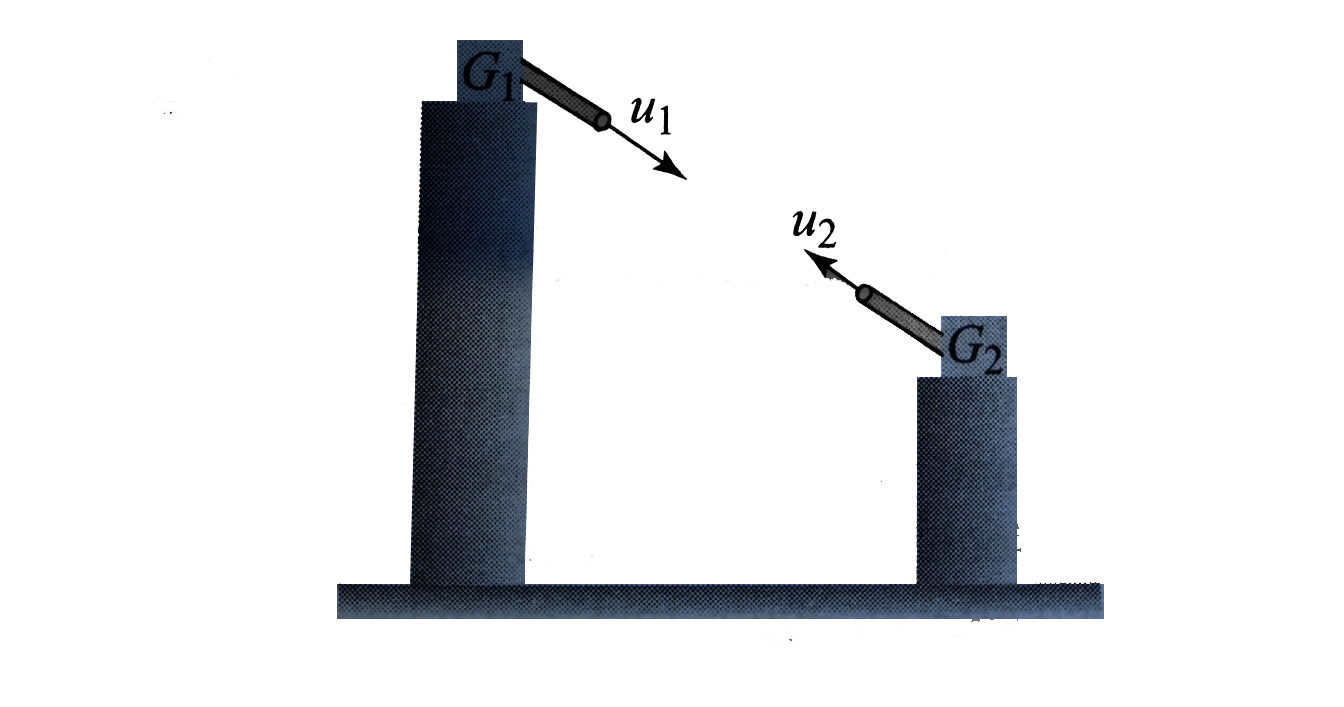
Two guns are mounted (fixed) on two vertical cliffs that are very high from the ground as shown in figure. The muzzle velocity of the shell from G1 is u1 and that from G2 isu2. Such that the shells collide with each other in air is (Assume that there is no resistance of air)
View SolutionAn arrow is shot into air. Its range is 200m and its time of flight is 5s. If g=10ms−2, then horizontal component of velocity and the maximum height will be respectively
View SolutionA missile is fired for maximum range with an initial velocity of 20m/s. If g=10m/s2, the range of the missile is
View Solution
