The $M . I .$ of a rod about an axis through its center and perpendicular to it is $I_{0}$ . The rod is bent in the middle so that the two halves make an angle $θ$ . The moment of inertia of the bent rod about the same axis would be

$I_{0} {sin}^{2} θ$

$I_{0} {cos}^{2} θ$

$I_{0}$

$\frac{I_{0}}{2}$

Video Solution

Text Solution

Verified by Experts

$I_{A} = \frac{M L^{2}}{12} = I_{0}$
Now rod is bent at $A$

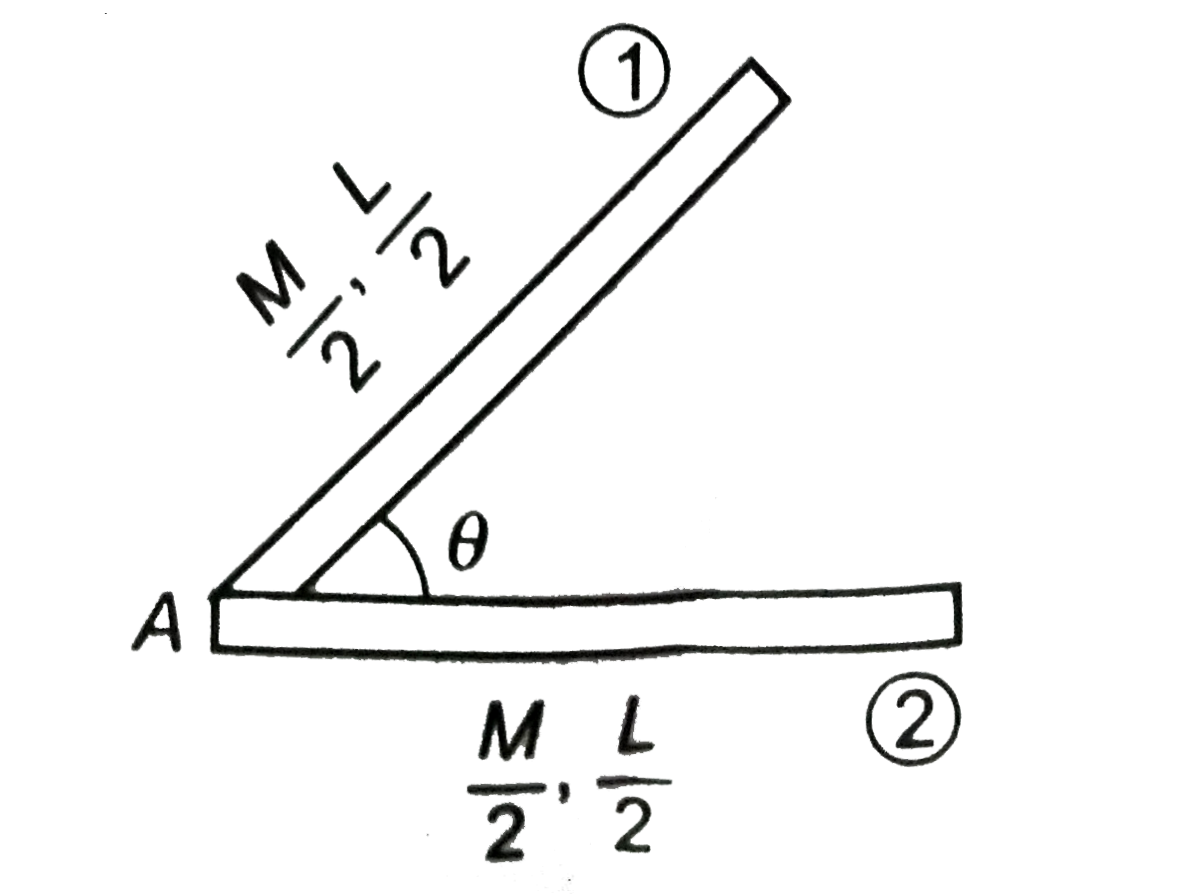
$M . I .$ of half rod ( $1$ ) about $A$ and $⊥^{a r}$ to the plane
$I_{1} = \frac{1}{3} \frac{M}{2} {(\frac{L}{2})}^{2} = \frac{M L^{2}}{24} = I_{2}$
$I_{A} = I_{1} + I_{2} = \frac{M L^{2}}{12} = I_{0}$
$M . I .$ will remain the same for any value of $θ$ .

Updated on:21/07/2023

The moment of inertia of a rod about an axis through its centre and perpendicular to it is 1/12ML² (where M is the mass and L is te length of the rod). The rod is bent in the middle so that the two halves make an angle of 60°. the moment of inertia of the bent rod about the same axis would be
A $\frac{1}{48} M L^{2}$
B $\frac{1}{12} M L^{2}$
C $\frac{1}{24} M L^{2}$
D $\frac{M L^{2}}{8 \sqrt{3}}$
The moment of inertia of a rod about an axis through its centre and perpendicular to it is $\frac{1}{12} M L^{2}$ (where, M is the mass and L is the length of the rod). The rod is bent in the middle so that the two halves make an angle of $60^{\circ}$ The moment of inertia of the bent rod about the same axis would be :
A $\frac{1}{48} M L^{2}$
B $\frac{1}{12} M L^{2}$
C $\frac{1}{24} M L^{2}$
D $(M L^{2}) ? (8 \sqrt{3})$
The moment of inertia of a rod about an axis through its centre and perpendicular to it is $\frac{1}{12} M L^{2}$ (where, M is the mass and L is the length of the rod). The rod is bent in the middle so that the two halves make an angle of $60^{\circ}$ The moment of inertia of the bent rod about the same axis would be :
A $\frac{1}{48} M L^{2}$
B $\frac{1}{12} M L^{2}$
C $\frac{1}{24} M L^{2}$
D $(M L^{2}) ? (8 \sqrt{3})$