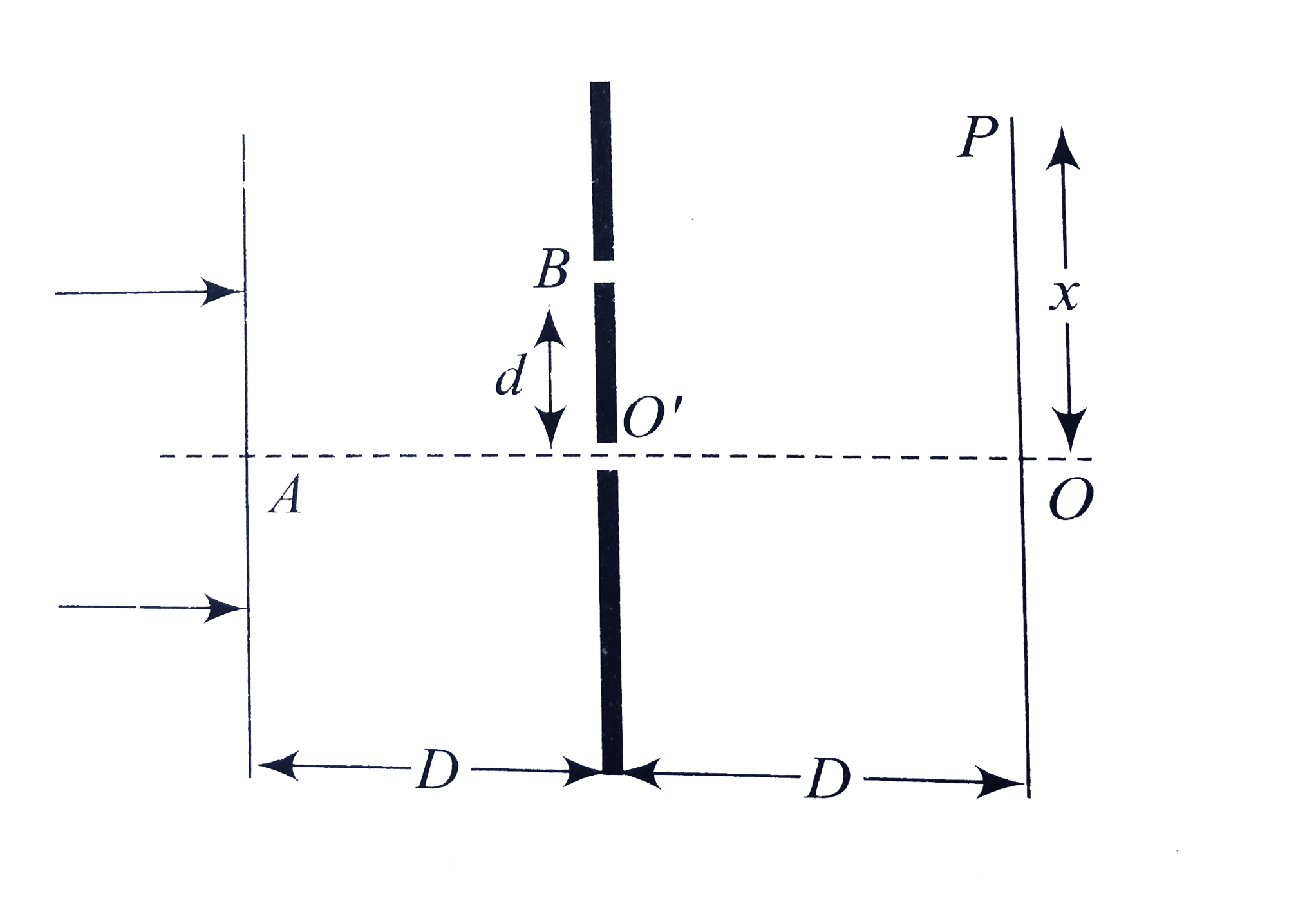
The minimum value of d so that there is a dark fringe at O is dmin. The distance at which are next bright fringe is formed is x. then

dmin=√λD
dmin=√λD2
x=dmin2
x=3dmin
The correct Answer is:B, D
There is dark fringe at O if the difference,
δ=ABO−AO.O=λ2
=2√D2+d2−2D
=2d22D=d2D=λ2
⇒dmin=√λD2
The bright fringe is formed at P if the path difference
δ.=AO.P−ABP=λ
=D+√D2+x2−√D2+d2−√D2+(x−d)2=λ
=x22D−d22D−(x2+d2−2xd)2D=λ
Given d=dmin
On solving, x=3dmin=3√λD2.
Topper's Solved these Questions
- WAVE OPTICSBOOK - MTG-WBJEECHAPTER - WAVE OPTICSEXERCISE - WB JEE PREVIOUS YEARS QUESTION (MCQ.s)
9 Videos
- THERMODYNAMICSBOOK - MTG-WBJEECHAPTER - THERMODYNAMICSEXERCISE - WB JEE Previous Years Questions
12 Videos
- WORK, POWER, ENERGYBOOK - MTG-WBJEECHAPTER - WORK, POWER, ENERGYEXERCISE - EXERCISE (WB JEE Previous Years Questions) CATEGORY 1 : Single Option Correct Type (1 Mark)
3 Videos
Similar Questions
The minimum value of d os that there is a dark fringe at O is dmin. For the value of dmin, the distance at which the next bright fringe is formed is x. Then
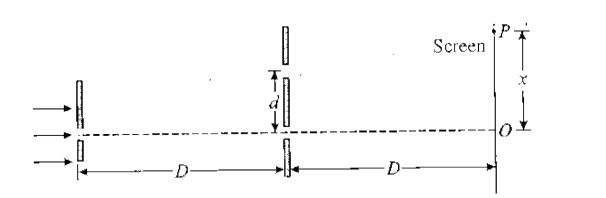
View SolutionConsider the arrangement shown in figure-6.38. The distance D is large compared to the separation d between the slits.
(a) Find the minimum value of d so that there is a dark fringe at O.
(b) Suppose d has this value. Find the distance x at which the next bright fringe is formed.
(c ) Find the fringe width.
View Solution
Knowledge Check
The minimum value of d os that there is a dark fringe at O is dmin. For the value of dmin, the distance at which the next bright fringe is formed is x. Then
 Admin=√λDBdmin=√λD2Cx=dmin2Dx=dmin
Admin=√λDBdmin=√λD2Cx=dmin2Dx=dminIn the arrangment shown in fin.

Find the distance x at which the next fringe is formed.A3λ2Bλ4Cλ2D5λ2In the double-slit experiment, the distance of the second dark fringe from the central line are 3mm. The distance of the fourth bright fringe from the central line is
A6mmB8mmC12mmD16mm
Consider the arrangement shown in figure. The distance D is large compared to the searated d between the slits. a. Find the minimum value of d so that there is a dark fringe at O. b. Suppose d has this value. Find the distance x at which the next bright firnnge is formed. c.Find teh fringe width.

View SolutionIn the arrangment shown in fin.

Find the distance x at which the next fringe is formed.
View SolutionIn a biprism experiment, the fringe width is 0.4mm. The distance between the fourthh dark fringe and the sixth bright fringe is
View SolutionFringe width equal to 1 mm is observed in the interference pattern of biprism experiment. Then the distance of nearest bright fringe from the central bright fringe will be :
View SolutionIn a double slit experiment , the coherent sources are spaced 2d apart and the screen is placed a distance D from the slits. If nth bright fringe is formed on the screen exactly opposite to a slit , the value of n must be -
View Solution
