The net magnetic flux through any closed surface, kept in a magnetic field is
zero
μ04π
4πμ0
4μ0π
The correct Answer is:A
To solve the question regarding the net magnetic flux through any closed surface kept in a magnetic field, we can follow these steps:
1. Understanding Magnetic Flux:
Magnetic flux (Φ) through a surface is defined as the product of the magnetic field (B) and the area (A) of the surface, projected in the direction of the magnetic field. Mathematically, it can be expressed as:
Φ=∫B⋅dA
where dA is a differential area vector.
2. Closed Surface Concept:
We are considering a closed surface, which means it completely encloses a volume. Examples include spheres, cubes, etc.
3. Gauss's Law for Magnetism:
According to Gauss's law for magnetism, the net magnetic flux through any closed surface is zero. This is expressed mathematically as:
Φ=∮B⋅dA=0
This implies that the number of magnetic field lines entering the closed surface is equal to the number of magnetic field lines leaving the surface.
4. Reasoning:
Magnetic field lines are continuous and do not begin or end at any point (they are always closed loops). Therefore, any magnetic field line that enters a closed surface must also exit it, resulting in a net flux of zero.
5. Conclusion:
Based on the above reasoning, we conclude that the net magnetic flux through any closed surface kept in a magnetic field is zero.
Final Answer:
The net magnetic flux through any closed surface kept in a magnetic field is 0.
---
Magnetic flux (Φ) through a surface is defined as the product of the magnetic field (B) and the area (A) of the surface, projected in the direction of the magnetic field. Mathematically, it can be expressed as:
Φ=∫B⋅dA
where dA is a differential area vector.
We are considering a closed surface, which means it completely encloses a volume. Examples include spheres, cubes, etc.
According to Gauss's law for magnetism, the net magnetic flux through any closed surface is zero. This is expressed mathematically as:
Φ=∮B⋅dA=0
This implies that the number of magnetic field lines entering the closed surface is equal to the number of magnetic field lines leaving the surface.
Magnetic field lines are continuous and do not begin or end at any point (they are always closed loops). Therefore, any magnetic field line that enters a closed surface must also exit it, resulting in a net flux of zero.
Based on the above reasoning, we conclude that the net magnetic flux through any closed surface kept in a magnetic field is zero.
The net magnetic flux through any closed surface kept in a magnetic field is 0.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - THE EARTH S MAGNETISM19videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - MAGNETISATION AND MAGNETIC INTENSITY11videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Assertion And Reason15videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason15videos
MOVING CHARGES AND MAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
Statement-1 The net magnetic flux through a spherical surface enclosing north pole of a bar magnet as zero
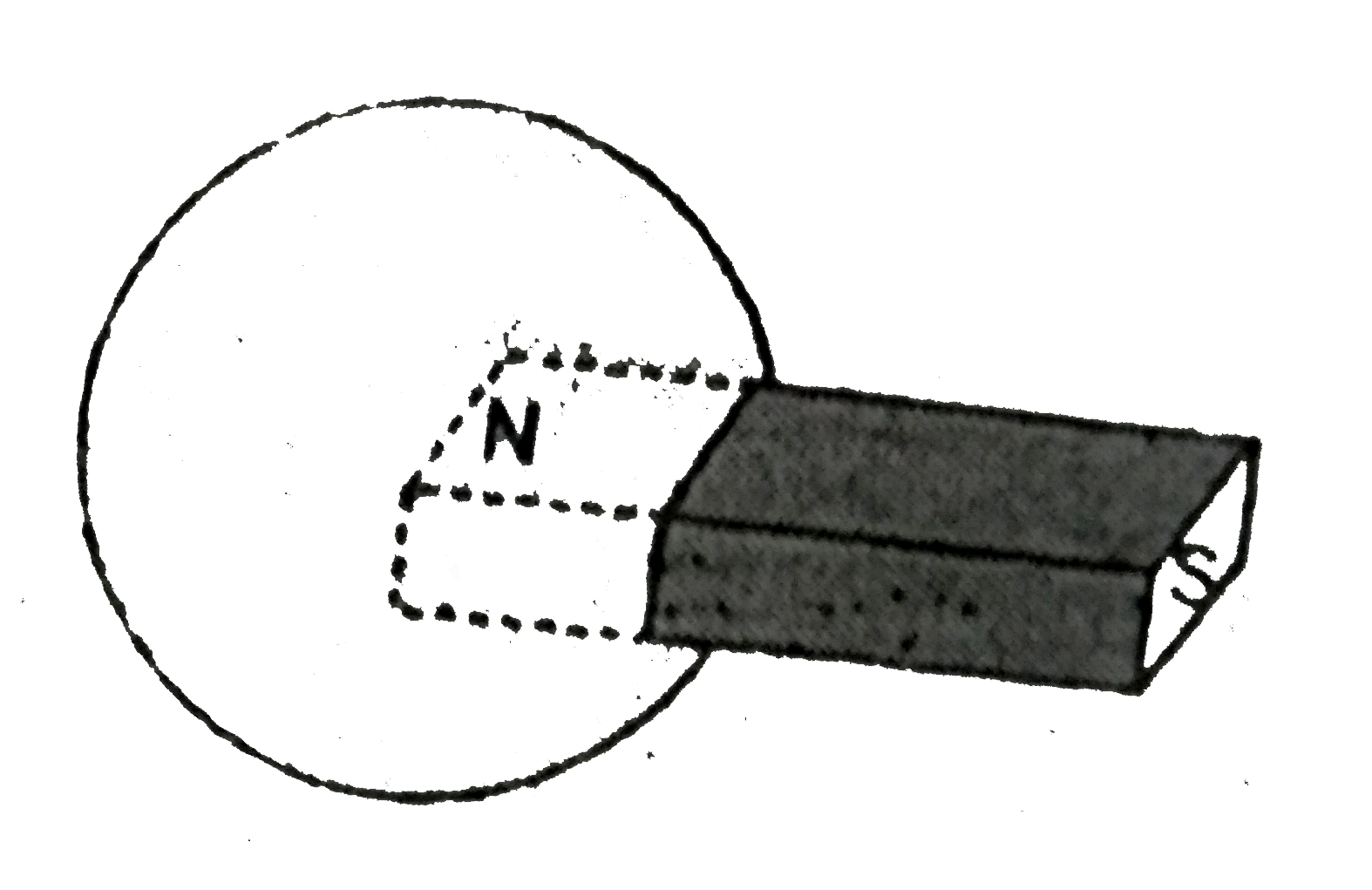
Statement-2 Magnetic field lines always form closed loopsAIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false. - Question 2 - Select One
Statement-1 The net magnetic flux through a spherical surface enclosing north pole of a bar magnet as zero

Statement-2 Magnetic field lines always form closed loopsAIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
Assertion: In a region where uniform electric field exists, the net charge with in volume of any size is zero.
Reason: The electric flux within any closed surface in region of uniform electirc field is zero.View SolutionStatement-1 The net magnetic flux through a spherical surface enclosing north pole of a bar magnet as zero

Statement-2 Magnetic field lines always form closed loopsView SolutionThe net flux passing through a closed surface enclosing unit charge is
View SolutionAssertion (A): The net magnetic flux coming out of a closed surface is always zero.
Reason (R ): Unlike poles of equal strength exist togetherView SolutionThe magnetic flux linked with a vector area →A in a uniform magnetic field →B is
View SolutionA capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
View Solution

