The plates of a capacitor of capacitance 10(μ)F,charged to 60(μ)C,are joined together by a wire of resistance 10(Ω)at t=0.Find the charge on the capacitor in the circuit at (a)t=0,(b)t=30(mu)s,(c )t=120(mu)s and (d)t=1.0ms.
To solve the problem step by step, we will use the formula for the charge on a discharging capacitor:
q(t)=q0e−tRC
where:
- q(t) is the charge at time t,
- q0 is the initial charge,
- R is the resistance,
- C is the capacitance,
- t is the time,
- e is the base of the natural logarithm.
Given Data:
- Capacitance, C=10μF=10×10−6F
- Initial charge, q0=60μC=60×10−6C
- Resistance, R=10Ω
Step 1: Calculate the time constant τ
The time constant τ is given by:
τ=R×C
Substituting the values:
τ=10Ω×10×10−6F=10×10−5=10−4s=100μs
Step 2: Calculate the charge at different times
(a) At t=0
Using the formula:
q(0)=q0e−0RC=q0
Thus,
q(0)=60μC
(b) At t=30μs
Using the formula:
q(30μs)=60×10−6e−30×10−610×10−6
Calculating the exponent:
−30×10−610×10−6=−3
So,
q(30μs)=60×10−6e−3
Using e−3≈0.0498:
q(30μs)≈60×10−6×0.0498≈2.988μC
(c) At t=120μs
Using the formula:
q(120μs)=60×10−6e−120×10−610×10−6
Calculating the exponent:
−120×10−610×10−6=−12
So,
q(120μs)=60×10−6e−12
Using e−12≈6.144×10−6:
q(120μs)≈60×10−6×6.144×10−6≈0.00036864μC
(d) At t=1.0ms
Using the formula:
q(1.0ms)=60×10−6e−1.0×10−310×10−6
Calculating the exponent:
−1.0×10−310×10−6=−100
So,
q(1.0ms)=60×10−6e−100
Using e−100≈3.720×10−44:
q(1.0ms)≈60×10−6×3.720×10−44≈2.232×10−48μC
Final Answers:
- (a) q(0)=60μC
- (b) q(30μs)≈2.988μC
- (c) q(120μs)≈0.00036864μC
- (d) q(1.0ms)≈2.232×10−48μC
- q(t) is the charge at time t,
- q0 is the initial charge,
- R is the resistance,
- C is the capacitance,
- t is the time,
- e is the base of the natural logarithm.
- Capacitance, C=10μF=10×10−6F
- Initial charge, q0=60μC=60×10−6C
- Resistance, R=10Ω
The time constant τ is given by:
Using the formula:
Using the formula:
Using the formula:
Using the formula:
- (a) q(0)=60μC
- (b) q(30μs)≈2.988μC
- (c) q(120μs)≈0.00036864μC
- (d) q(1.0ms)≈2.232×10−48μC
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
The plates of a 50(μ)F capacitor charged to 400(μ)C are connected through a resistance of 1.0k(ohm). Find the charge remaining on the capacitor 1s after the connection is made.
View SolutionThe plates of a capacitor of capacitance C are given the charges Q1andQ2 as shown in figure. Now the switch is closed at t =0. Find the charges on plates after time t.
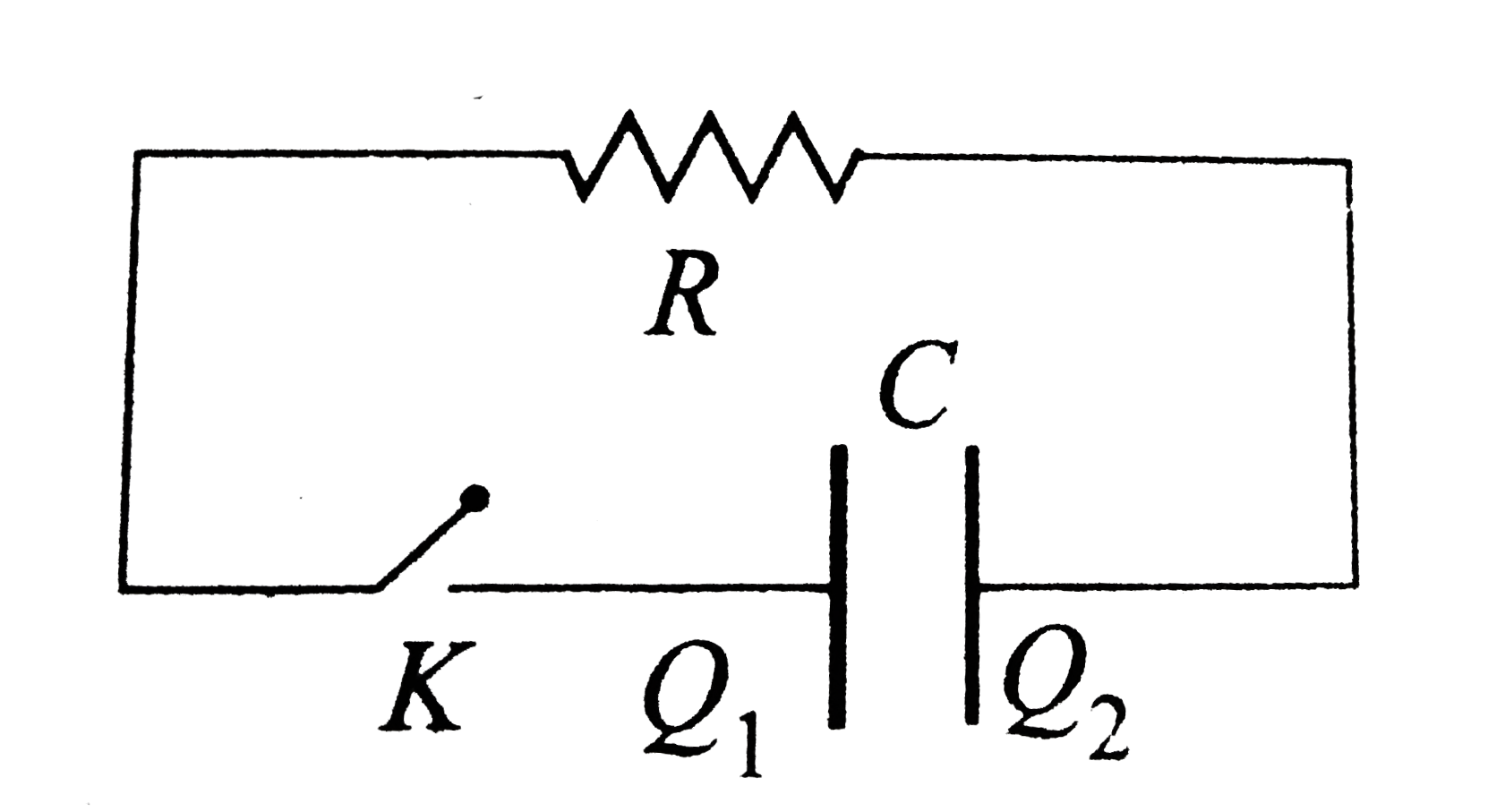
View SolutionThere is no resistance in the capacitive circuit shown. Then charge on the capacitor at an time t

View SolutionIn steady state, find the charge on the capacitor in (μC) shown in figure.
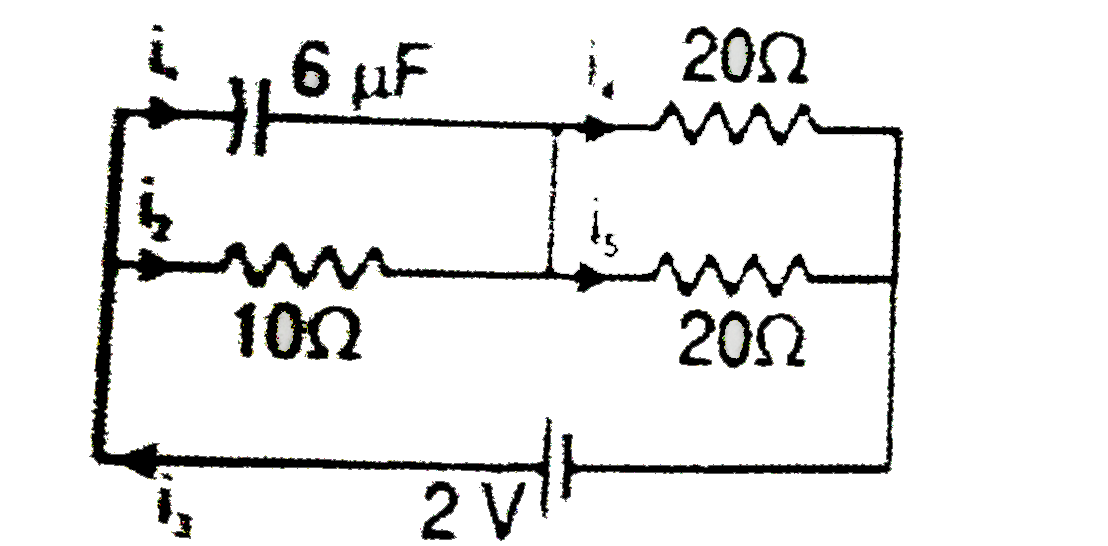
View SolutionA 20(μ)Fcapacitor is joined to a battery of emf 6.0V through a resistance of 100(Ω).find the charge on the capacitor 2.0ms after the connections are made .
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA 4μF capacitor is charged to 400 volts and then its plates are joined through a resistor of resistance 1KΩ. The heat produced in the resistor is
View SolutionA 4μF capacitor is charged to 400 volts and then its plates are joined through a resistor of resistance 1KΩ. The heat produced in the resistor is
View SolutionA 5.0(μ)F capacitor having a charge of (20(μ)C)is discharged through a wire aof resistance (5.0Ω). Find the heat dissipated in the wire between 25 to 50 (mu)s after the connections are made.
View Solution
